I preliminary has a list of about 16 unique problems I will present, but first a broad overview of the principal philosophy behind TGD. Later I will deepen the explanations, so please try to consider only the blogposting in your debate. Questions are welcome, and I will later come back to questions I cannot answer immidiately. This will be also my own learning process.
I have discussed these things very loosely on a FB group, and they rejected the theory, but their reasons were not immidiately acceptable by me. I don't reject objections, and critique are welcome. I will study all objections as far as I can.
I make this in blogformat and if the trial don't work well I can delete the blog.
I meant to publish on Matti Pitkänens birtday (but family problems turned in) so 'Happy birthday' Matti. Hope you will find this blog enjoyable.
To the lessons.
TGD lesson 1.
TGD, a theory of trinity (a triality).
Topological Geometro Dynamics is a theory about interactions, and relies heavily on geometric ideas. The geometrization of fundamental interactions assuming that space-times are representable as effective 2-dimensionality and stringy worlds sheets and partonic 2-surfaces at 4-D space-time surface of M4×: CP2 as basic structures, is wherefrom everything began. Interactions depends on strings/braids.
The basic physical picture behind TGD was formed as a fusion of two rather disparate approaches that thereafter were unified and led to the notion of the many-sheeted space-time:
- TGD is as a Poincare invariant theory of gravitation obtained by fusing Special and General Relativities. The representation of space-time surface is a hyperquaternionic sub-manifold of hyperoctonionic space. Note that "straight lines" would correspond to light-like geodesics of the 8-D imbedding space reducing to those of 4-D Minkowski space. Light-like geodesics would correspond to those of space-time surface. These are unified in TGD.
- TGD as a generalization of the old-fashioned hadronic string model, obtained by replacing 1-dimensional strings with 3-surfaces.
- TGD as a generalized number theory. Infinite primes (one end open) and p-adicization are basic pillars of the vision. Gauge coupling evolution is replaced with p-adic coupling constant evolution which occurs as jumps at half octaves of the basic mass scale. Squared thermodynamics also important.
Relies also on quaternions and is restricted to *flat* 3-space (or Euclidian 4-space). This does *not* allow a description of gravitation. Already Riemann realized that one needs the notion of curved space to understand everyday macroscopic world and a mathematization of the notion of length measurement, and performed the needed generalization.
The idea of quaternionicity of space-time: it is one of the cornerstones of TGD. The notion must be however refined to allow curved space-time and gravitation. This requires the identification of space-time as 4-surface (as instance neutrino super-luminality?).
The notion of quaternionic space-time surface in octonionic space-time and quaternionicity as a local property of the tangent space determining the classical dynamics.
The latest conjecture inspired by the effective 2-dimensionality is that real Euclidian contribution reduces to the total area of partonic 2-surfaces and the purely imaginary contribution from Minkoskian regions to that for string world sheets. String world-sheet - partonic 2-surface duality would suggest that the magnitudes of these contributions are actually identical.
To this I will would put my money if I had money;-)!, says Matti.
The basic idea?
Matti Pitkänen was inspired of among all Penrose’s thinking (Penrose does argue that chaotic processes are themselves algorithmic (Penrose 1994: 177-179), in that they can be simulated to any desired degree of accuracy by digital computational mechanisms) about reality composed of interactions among the three worlds.Using the Gödel Incompleteness theorem the worlds have to be three, a classic, a quantum and an incomplete, unknowable, see also Caitlin the Unknowable. A consequence of Penrose's Gödel-inspired arguments for strong (no-algorithm-can- even-approximate) noncomputability in the mind/brain is that current theories in physics are fundamentally incomplete. This is essential in TGD. We will never get the complete theory because everything evolves. Others also has this view, there will never be any absolute TOE.
Because certain cognitive processes - including those responsible for mathematical knowledge - are nonalgorithmic, while all classical level biochemical processes are algorithmic. The central motivation, therefore, underpinning Penrose's whole argument structure is a problem in the epistemology of mathematics. It is the problem of how we understand mathematics (understanding does not consist in following a rule) as the meaning of mathematical concepts. This requires a self and consciousness (and cognition, qualia) in TGD.

Figure 1: Penrose's Three Worlds. The drawing schematically illustrates the idea that the Physical World can be thought of as a projection from part of the Platonic World of eternal Truths, the Mental World arises from part of the Physical World (presumably the brain), and that the Platonic World is 'grasped' somehow during some mental activities. "Shadows of the Mind" 1994.
"There is the Physical world, out of which a tiny part make out Mental worlds, out of which a world of Platonic ideas emerge, mathematics being just a small part of it, and physically relevant mathemathical theories a smaller part of the mathematical whole, yet that small part is in principle enough to generate the whole of the physical world." In "The Road to Reality" 2005. Parallell to or derived from Popper-Eccles three worlds (with psychons).
Penrose points out that quantum mechanism consists of two processes, one referred to as U is completely deterministic, classic, involving the evolution of the solution according to the Schrödinger equation; the other, the reduction part R is the one that leads to the problems of the thorny issues of the involvement of the observer, to which various subtle interpretations have been applied, notably the Copenhagen interpretation. Penrose thinks quantum theory is incomplete (and conflicts with Einsteins GR theory). Penrose is also very critical to string theory ("the only game in town") and he likens the enterprice to a groupof hapless tourists exploring a beautiful city in search for a beautiful garden, none of them understanding the local language, with no maps available, and with only aesthetic criteria as guidelines, and the trust in the guru-like intution of their leader (Witten). Indeed, in the absence of direct physical confirmations, the only guiding ideas being those of mathematical beauty, and this should be noted being a fact of life and not a choise. Weyl, Dirac, (Einstein)... stubbornly hold to beauty instead of truth. Also Penrose held beauty as guideline. His twistors are not as magical, though, as string-theory. String-theory doubts the nature of objective science, and string-theory is not a theory of Physics, rather then by Maths.
 Figure 2. Compare a 3-knot.
Figure 2. Compare a 3-knot.From this trinity arose in TGD with Pythagorean triplets and its squares, and the geometry, the knots, polytopes and quasiparticles with consciousness and biology as necessary parts. Self determines the decay by topology (entangled states as ‘memory’). Everything is very symmetric, topologic and very deeply fractal and geometric, also fields and elemental particles. p-Adic physics provides space-time correlates for cognition and intentionality.
Dragovich in a review 2003:
p-Adic mathematical physics emerged as a result of efforts to find a non-Archimedean approach to the spacetime and string dynamics at the Planck scale. One of its main achievements is a successful formulation and development of p-adic and adelic quantum mechanics, which have complex-valued wave functions of p-adic and adelic arguments. As a result of adelic approach, p-adic effects exhibit a spacetime and some other discreteness, which depend on the adelic quantum state of the physical system under consideration. ”Which aspects of the Universe cannot be described without use of p-adic numbers ?” According to the uncertainty, it is not possible to handle distances shorter than 10^−33cm and consequently one cannot apply only Archimedean geometry beyond the Planck length. There is a generic quantum gravity uncertainty for possible measurements of distances approaching to the Planck length ℓ0, which restricts priority of Archimedean geometry based on real numbers and gives rise to employment of the non-Archimedean one related to p-adic numbers… Since wave functions are complex-valued, one cannot construct a direct analogue of the Schrödinger equation with a p-adic version of Heisenberg algebra. p-Adic quantum mechanics is given by a triple (L2(Qp),Wp(z), Up(t)) .The non-commutativity of p-adics can be overcome. p-Adic strings are modelled in "On p-Adic Mathematical Physics" by Dragovich et al., with three possibilities. Venetziano amplitude (triality, Susy), an analogue of the crossing symmetric Veneziano amplitude (the Gel’fand-Graev beta function) and generalization described by nonlocal effective field theories. Find Dragovich works on arXive. Witten is also one of the authors behind p-adic strings.
Group relations can be straightforwardly generalized, including p-adic cases, by replacing formally index infinity by v (reals). Adelic quantum mechanics is a natural generalization of the above formulation of ordinary and p-adic quantum mechanics. Recall that an adele x is an infinite sequence, see Vladimirov and Volovich.
Bott periodicity contains these numbers in a hidden configuration. Bott's original proof (1959) used Morse theory, which Bott had used earlier to study the homology of Lie groups. "An application of the Morse theory to the topology of Lie-groups"
See and compare as instance to Caponio et al. 2010, Morse theory of causal geodesics in a stationary spacetime via Morse theory of geodesics of a Finsler metric:Dragovich, p 10. The main task of quantum cosmology is to describe the very early stage in the evolution of the Universe. At this stage, the Universe was in a quantum state, which should be described by a wave function. Usually one takes that this wave function is complex-valued and depends on some real parameters. Since quantum cosmology is related to the Planck scale phenomena it is natural to reconsider its foundations. We maintain here the standard point of view that the wave function takes complex values, but we treat its arguments (spacetime coordinates, gravitational and matter fields) to be not only real but also p-adic and adelic. World-sheet, string momenta and amplitudes are manifestly p-adic. Since string amplitudes are p-adic valued functions, it is not so far enough clear their physical interpretation.
... the index of a lightlike geodesic in a conformally standard stationary spacetime (M0×R,g) is equal to the index of its spatial projection as a geodesic of a Finsler metric F on M0 associated to (M0×R,g). Moreover we obtain the Morse relations of lightlike geodesics connecting a point p to a curve γ(s)=(q0,s) by using Morse theory on the Finsler manifold (M0,F). To this end, we prove a splitting lemma for the energy functional of a Finsler metric. Finally, we show that the reduction to Morse theory of a Finsler manifold can be done also for timelike geodesics.
The existence of quasicrystals is evidence for an unrecognized, nonalgorithmic physical process, thought Penrose. That went further to knot-theories. Non-periodic sets tile the plane with a five-fold symmetry, which gives problems with growth. Discovered by Dan Shechtman, Nobelist 2011, "quasicrystals have changed our view of what matter can be". Until the 1980s, they were disregarded in favor of the prevailing views about the atomic structure of matter. Hundreds of quasicrystals have been reported and confirmed today. Quasichrystals as surface plasmons can invoke on dispersion and give a low velocity to get slow light, which gives higher efficiency of light adsoption, tells Baez (week 293). The refractive index of a substance is the inverse of the speed of light in that substance. The 24-cell and Atiyahs magic square also belong here.
 Figure 3. The 24-cell, inscribed in a 3-sphere of radius √2. When interpreted as the quaternions, the F4 root lattice (which is integral span of the vertices of the 24-cell) is closed under multiplication and is therefore forms a ring. This is the ring of Hurwitz integral quaternions. The vertices of the 24-cell form the group of units (i.e. the group of invertible elements) in the Hurwitz quaternion ring (this group is also known as the binary tetrahedral group). The vertices of the 24-cell are precisely the 24 Hurwitz quaternions with norm squared 1, and the vertices of the dual 24-cell are those with norm squared 2. The D4 root lattice is the dual of the F4 and is given by the subring of Hurwitz quaternions with even norm squared. Translating the four-dimensional coordinates into quaternions, the points of an appropriately scaled and orientated 24-cell form a multiplicative group. Wikipedia.
Figure 3. The 24-cell, inscribed in a 3-sphere of radius √2. When interpreted as the quaternions, the F4 root lattice (which is integral span of the vertices of the 24-cell) is closed under multiplication and is therefore forms a ring. This is the ring of Hurwitz integral quaternions. The vertices of the 24-cell form the group of units (i.e. the group of invertible elements) in the Hurwitz quaternion ring (this group is also known as the binary tetrahedral group). The vertices of the 24-cell are precisely the 24 Hurwitz quaternions with norm squared 1, and the vertices of the dual 24-cell are those with norm squared 2. The D4 root lattice is the dual of the F4 and is given by the subring of Hurwitz quaternions with even norm squared. Translating the four-dimensional coordinates into quaternions, the points of an appropriately scaled and orientated 24-cell form a multiplicative group. Wikipedia.Other Nobelists have used the 3-worlds picture about consciousness. Is consiousness emergent or transcendent? Sperry and Eccles three worlds in biology, physical, mind or psyche (soul) and knowledge (social reality) were their examples for 3-worlds, from Popper 1934. See Poppers three worlds from 1978, the universe is composed of two essential substances: Res Cogitans and Res Extensa, used by Stuart Kauffman. This is not causation though, but some kind of epiphenomalism. Intentions and consciousness are pointed out. C.-G. Jung is also important. Terms as collective unconsciousness and racial memory were used by Eccles.
This brings consciousness and memory by force out of body, which is a cornerstone in TGD. Consciousness is created in the measurement from cognitive elements (as p-adics) outside the ‘reality’, and can only be diminished and transformed into awareness that grows as the possibilities diminish. Quantum jump has a complex anatomy since it must include state preparation, state function reduction, and unitary process characterized by U-matrix. Zero energy ontology (ZEO) means a distinguishion between U-matrix and M-matrix (timelike entanglement), identified as a "complex" square root of density matrix representable as a product of its real and positive square root and of unitary S-matrix so that thermodynamics becomes part of quantum theory with thermodynamical ensemble being replaced with a ZEO-state. The unitary U-matrix describes quantum transitions between zero energy states and is therefore something genuinely new. >U<-matrix is natural sign for statistical description of intentional action. The physical world is seen as a condensate from the geometric world and dark matter. The geometric, symmetric figures and numbers, real and non-real, and fractals, give birth to the consciousness and representations of the environment to self, due to quantum jumps or possibilities, information in patterns, made real in the jump or measurement, and giving rise to the space in the braiding process. Quantum jump remains the only purely quantal aspect of quantum theory in this approach since there is no quantization at the level of the configuration space.
| Physical world | Mental world | Platonic world |
| *Classic | *Quantum (Ether, grid, psi, subtle energy) | *Incomplete, noncomputable, nonalgoritmic |
| Biochemistry | Understanding | Cognition |
| Particle, a condensate | Wave | String |
| Brain | Truth | Meaning , Grasped |
| Proton capturers, ATP S-matrix | Memory, dreams M-matrix | Consciousness, life, memory-DM, U-matrix |
| #Classic world | #Quantum world | #Psychologic, geometric world |
| Laws, rules of own, lifetimes measured | Laws, rules of own, light-like cone, measured? | Laws, rules of own, not measured, potential, bond |
| Quantized, descreate Hidden structure? | Plancks const^2 – DM, expanded, finite, generalized | Supersymmetry (TGD-variant) |
| Real abelian numbers/algebra | Non-abelian numbers/algebra | Primes, p-adics, transcendentals |
| Body, representations, body maps, the Big Book, WCW | Mind | Self, hierarchic, changing, collective consciousness |
| Perception, | Intention | Qualia |
| Time, objective holography | Time, subjective; all times Generalized holography | Holography |
| Physical condition | Energetic condition | The zero point, ZEO, ‘nothing’ |
| Tool | Frame, interpretation | Meaning, pattern, entropy-negentropy, information |
Some general charachteristics of the 3-worlds. *= Penrose, # = TGD. Generalizations are in yellow. This scheme is only approximate. P-adics should as instance also be found in classic world.
A mathematically beautiful idea must have been adopted by God, says Dirac. Is harmony and beauty a reason? Are numbers real or invented? TGD takes the view both are true, and we should trust our observations. Numbers can be seen as an hierarchic, infinite tree-like structure (p-adic integers are open, infinite, expressing a matrix or string back to big bang with a knot (particle) at the other end toward us), forming superstructures and supersymmetries as hidden massive DM. The branch is the nearest neighbor, not the nearest formation, which may be more close, hence the DM-control. Beneath the lattice is the geometry forming a ‘lightcone’ (ZEO). See also J. Graves `eight squares theorem' and Bott periodicity and non-associativity, described in Octonions by Baez. TGD is squared thermodynamics, expressing an hierarchy symmetry. The branching is guided by primes, forming groups or categories, hence the name causal diamonds. These describes the history as a world-line or space-time sheat back in time. Space contains many of these sheats. Squared bubbles within bubbles is another picture.
Some numbers:
- Perfect numbers as primes. If as many numbers as we please beginning from a unit be set out continuously in double proportion, until the sum of all becomes a prime, and if the sum multiplied into the last make some number, the product will be perfect.
- Fermat? - a number multiplied by itself (2 x 2=4) produced the square. The square root of a number led back to the original number that was squared (the square root of 4 = 2 or -2, since -2 x -2 also = 4). Any positive integer, all of whose odd prime factors congruent to 3 modulo 4 occur to an even exponent, is expressible as a sum of two squares. Fermat's
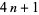 theorem, sometimes called Fermat's two-square theorem or simply "Fermat's theorem," states that a prime number
theorem, sometimes called Fermat's two-square theorem or simply "Fermat's theorem," states that a prime number 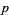 can be represented in an essentially unique manner (up to the order of addends) in the form
can be represented in an essentially unique manner (up to the order of addends) in the form 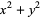 for integer
for integer  and
and 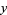 iff
iff 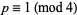 or
or 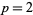 (which is a degenerate case with
(which is a degenerate case with 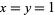 ).
). - Euler's four-square identity the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. infinite descent
- Götzkys four square theorem: Two-squares and four-squares representation theorems for the rational integers were asserted by Fermat in the 1600s and first publicly proved by the efforts of Euler and Lagrange in the 1700s. Fermat’s claim that all positive rational integers were sums of three triangular numbers, four squares, five pentagonal numbers, etc., was established by Cauchy in the early 19th century. In 1928, Götzky proved that all totally positive integers in Q(√ 5 ) were the sum of four squares of algebraic integers from that field. Also, results about the representation of primes by sums of two squares are obtained for Q (√ 5 ) . We must consider a lattice in R8 for the analogous four-squares theorem.
- Graves eight squares theorem: After the discovery of quaternions Graves employed himself in extending to eight squares Euler's theorem that the sum of four squares multiplied by the sum of four squares gives a product which is also the sum of four squares, and went on to conceive a theory of "octaves" (now called octonions) analogous to Hamilton's theory of quaternions, introducing four imaginaries additional to Hamilton's i j k, and conforming to ‘the law of the modulus'. Graves devised also a pure-triplet system founded on the roots of positive unity.
- Baez: the product of two sums of 8 perfect squares is again a sum of 8 perfect squares. The complex numbers and quaternions allow one to prove similar theorems for 2 and 4 squares. Graves considered the idea of a general theory of "2m-ions".
TGD general view.
TGD arises from an intense interaction between the geometry, p-adics algebra, consciousness, a generalized number theory (infinite primes and p-adics) and the dynamic Planck constant hierarchy of matter-DM. Result: World of classical worlds (WCW), the unique TGD-Universe with a book-like structure. Time and energy gets doubled, reversed. Einsteins space concept is too simple, now causal diamonds, CDs. The new p-adic time scales (as 10-fractions or the five-fold symmetry?) gives biocontrol and coherence. The general theory for particle massivation is based on p-adic thermodynamics (HFFs) Hierarchy is based on p-adic length. p-Adics length and time scales are made sensitive by an integer. The work with HFFs combined with experimental input led to the notion of hierarchy of Planck constants interpreted in terms of dark matter. The conflict between the non-determinism of state function reduction and determinism of time evolution of Schrödinger equation is serious enough a problem to motivate the attempt to extend physics to a theory of consciousness by raising the observer from an outsider to a key notion also at the level of physical theory. See number theoretic realization of compactification.
TGD tries to unify fundamental interactions (in 5 threads) by assuming that physical space-times can be regarded as sub-manifolds of certain 8-dimensional space, which is product of Minkowski space and 4-dimensional complex projective space CP2 (Quaternion, I get a Dirac cone in mind, a double Lorenzian 4D universe). To have that the strings (interaction sites) must be hadrons = 3-dimensional light-like surfaces (= with reversed time too). One outcome is the notion of many-sheeted space-time (WCW) involving notions like topological field quantization and field body (and zero energy ontology, which was a necessary consequence). The huge conformal symmetries of the theory are essentially due to the light-likeness of 3-surfaces. And an 1D string cannot hold a self, only transfer interaction??? Singularities and monisms are problematic in TGD.
The empirically motivated generalization of quantum theory by introducing hierarchy of Planck constants forces a generalization of imbedding space to a book like structure and different pages of the book corresponds to macroscopic quantum phases which behave relative to each other like dark matter (invisible but gravitional). This can maybe be seen as analog to modified hidden/extra dimensions? The pages are dark in respect to each other.
Minkowskys cone as an attempt to construct Poincare invariant theory of gravitation (Poincare group acts in imbedding space rather than on space-time surface) [with Lorentz transformations], CD-diamonds. This gives the uncertainty and non-locality?
This frame addresses the unsolved problems of time, DM , consciousness, the observer-effect (SR) and the collective, the applications of TGD ranging from Planck length scale to cosmology (GR), and of living matter as a macroscopic quantum system.
TGD has a classic, quantum and biological frame. Biology is telling about the realizations of the two other frames. The most interesting new physics is related to how bio-systems manage to be macroscopic quantum systems. The recent formulation of quantum TGD proper relies heavily on the basic principles of TGD inspired theory of consciousness.
ZEO combined with the notion of finite resolution to an almost unique generalization of S-matrix (M-matrix) defined as Connes tensor product identified as time-like entanglement coefficients between positive and negative energy parts of zero energy states. A unification of thermodynamics and quantum theory is obtained. One prediction is the assignment of new macroscopic time scale to elementary particles: in case of electron this corresponds to 10 Hz fundamental biorhytm.
The new view about relationship between experienced and physical time allows to resolve the basic paradox of quantum measurement theory.
Interpretation for p-adic regions is as correlates for intentional action and cognition and thus the mind stuff of Descartes (world 3).
Topological Geometrodynamics, Books.
Overview. Over 1000 pages. Vixra 09008,0014v1
Quantum TGD as Infinite-Dimensional Spinor Geometry geometry of the "world of classical worlds"
Towards S-Matrix (unification =quantum gravity); finite measurement resolution
Physics as Generalized Number Theory, associativity as fundamental dynamical principle; space-time decomposes into real (body) and p-adic regions (cognition). It became clear that p-adicity leads to precise predictions for elementary particle masses and it is possible to understand the origin of the elementary particle mass scales number theoretically.
Classical Physics in Many-Sheeted Space-Time, almost topological quantum field theory
p-Adic Length Scale Hypothesis and Dark Matter Hierarchy
TGD and Fringe Physics
Consciousness and quantum biology. Books.
TGD Inspired Theory of Consciousness The notion of self replaces the notion of observer
Bio-Systems as Self-Organizing Systems an infinite self hierarchy having interpretation in terms of collective levels of consciousness
Quantum Hardware of Living Systems models for qualia, sensory representations, intentional action, etc.
Bio-Systems as Conscious Holograms The generalization of quantum hologram principle is crucial common concept.
Mathematical Aspects of Consciousness The fusion of real and p-adic physics (body and mind) to single coherent whole forces a generalization of number concept obtained by gluing real and p-adics along rationals and common algebraics.
Important generalizations in TGD makes it a very coherent and different theory:
- a Poincare invariant theory of gravitation - the representation of space-time surface as a hyperquaternionic sub-manifold of hyper-octonionic space
- strings with 3-surfaces. These two forces to form other generalizations
- p-adicization, p-adic strings/sheats
- a generalized number theory with infinite primes and p-adics
- Zero energy ontology (ZEO)
- U-matrix
- View of time
- the Big Book
- generalized holography
- Plancks const^2 = DM,
- P-adic time control
- Biosystems as macroscopic quantum systems
- Negentropy Maximization Principle (NMP)
- Everything is conscious and has selves
- A magnetic field body
- Life as islands of rational/algebraic numbers in the seas of real and p-adic continua
I’ll try to make a different post on each of these generalizations. To make the whole thing better understandable I want your feedback, thanks. Also negative are welcome, not trash though.
At last: Classical non-determinism makes possible time-like entanglement and cognitive states. Without classical non-determinism TGD would reduce to a string model. If string models were correct, our Universe would not be able to form self representations and there would be no string theorists. 24.4.2005 The world of classical worlds is zero-dimensional.
Cumrun Vafa has said, "I think that a reformulation of quantum mechanics which will resolve many of its puzzles is just around the corner. I think many share the view that the recently uncovered dualities point toward a new, more geometrical framework for quantum mechanics, in which space, time, and quantum properties will be inseparably joined together."
Edward Witten, "I believe the logical status of quantum mechanics is going to change in a manner that is similar to the way that the logical status of gravity changed when Einstein discovered the equivalence principle. This process is far from complete with quantum mechanics, but I think that people will one day look back on our epoch as the period when it began." [From 1998 interviews/chats of Brian Greene with Vafa and Witten.]
Witten: A new look at the path integral of quantum mechanics ... depends on topological string theory… At any rate, Witten simply takes a path integral and complexifies its phase space coordinates p and q. Visually, the dimension of the phase space gets doubled.
Some references:
Aityah, M.From_Algebraic_Geometry_to_Physics.
M.V.Altaisky and B.G.Sidharth,p-Adic physics below and above Planck scales.
Bott 1956,An application of the Morse theory to the topology of Lie-groups.
Baez, Octonions.
Caitlin, The Unknowable
Connes, A. 1994, Non-commutative geometry, Academic Press, ISBN 0-12-185860-X.
Branko Dragovich 2003: p-Adic and Adelic Quantum Mechanics. preprint only.B. Dragovich, A. Yu. Khrennikov, S. V. Kozyrev, I. V. Volovich , 2009. On p-Adic Mathematical Physics
Eccles, 1994, How the Self Controls Its Brain. see also wikipedia
Nobel lecture 1943: The ionic mechanism of postsynaptic inhibition
J. Graves `eight squares theorem'
Rick Grush and Patricia Smith Churchland, Gaps in Penroses toilings.
Gödel Incompleteness theorem,
Penrose, R. 1994 Shadows of the Mind, Shadows of the Mind on wikipedia
The Emperors New Mind, The Emperor’s New Mind on Wikipedia
2005, The Road to Reality, review on wikipedia
Pitkänen, M, 2009, Comments about M-matrix and Connes tensor product.
Pitkänens homepage 2011: TGD as a Generalized Number Theory II: Quaternions, Octonions, and their Hyper Counterparts
p-Adic Numbers and Generalization of Number Concept
Was von Neumann Right After All?
Popper 1934. The Logic of Scientific Discovery, 1978, Three Worlds, Popper, K. & Eccles, J. The self and its brain: An argument for interactionism. Berlin: Springer International, 1977.
Radagast-blogger, 2011: Three worlds.
Daniel da Rocha, Laurent Nottale, 2003: Gravitational Structure Formation in Scale Relativity,
D. Shechtman, I. Blech, D. Gratias, and J.W. Cahn, “Metallic Phase with Long-Range Orientational Order and No Translational Symmetry.” Physical Review Letters 53, 1951 (1984). Dan Shechtman, a video
Sperry, R. W. Mind-brain interaction: Mentalism, Yes; Dualism, No. Neuroscience, 1980, 5, 195-206. Roger Sperry , Left Brain: Right Brain, wikipedia, references, Nobel 1981, Some Effects of Disconnecting the Cerebral Hemispheres.
V. S. Varadarajan 2006. Has God made the quantum world p-adic?
Witten, E. 2010:A new look at the path integral of quantum mechanics
V.S. Vladimirov, I.V. Volovich, 1989: p-Adic QuantumMechanics, Commun. Math. Phys. 123: 659-676.
C. N. Yang, M. L. Ge 1989: Braid Group, Knot Theory, and Statistical Mechanics, WorldScientific.
TGD diary blog:
AdS/CFT does not work well for heavy ion collision...
http://matpitka.blogspot.com/2011/10/3-jet-and-9-jet-events-as-further.html
http://matpitka.blogspot.com/2011/10/is-k-action-expressible-in-terms-of.html