Poincare and Einstein, two giants.

"If we were not ignorant there would be no probability, there could only be certainty. But our ignorance cannot be absolute, for then there would be no longer any probability at all. Thus the problems of probability may be classed according to the greater or less depth of our ignorance. "Mathematics is not the study of objects, but instead, the relations (isomorphisms for instance) between them.

"Good theories are flexible. Those which have a rigid form and which can not change that form without collapsing really have too little vitality. But if a theory is solid, then it can be cast in diverse forms, it resists all attacks, and its essential meaning remains unaffected. The objections to them, therefore, far from annihilating them, actually serve them, since they allow such theories to develop all the virtues which were latent in them. The theory of Lorentz is one such " (My comment; TGD is usually accused for being a flexible theory).

Henry Poincaré


There has been no Nobel Prize awarded for the theory of relativity? Got the wrong man the Nobel Prize? Poincare was dead, otherwise he would have, [Lorentz (Nobel 1902 for his electron), Michelson (Nobel 1907), Minkowski (?), Planck (Nobel 1918)] the prize shared with Einstein (Nobel 1921)?

Would this have made the history go otherwise? Henri Poincaré died from embolism and cancer in 1912.

When the Michelson–Morley experiment failed to show the presence of “lumineferous ether” (if the ether did exist, the experiment would show that light moving in the same direction as the Earth was traveling faster than light moving at right angles to it) the physics community began a scramble to account for the findings, and took Einstein to unravel the mystery and a new era of physics was born. In fact Poincare was the one starting doubt the 'ether' and its 'dragging effect'.

The Relative Motion of the Earth and the Luminiferous Ether (1881)
On the Relative Motion of the Earth and the Luminiferous Ether (1887)
The Theory of Electrons and the Propagation of Light (1902)

At the end of the 19th century, when the detection (at the second order) by the Michelson Morley experience of the absolute motion “in the ether” of the Earth failed, the science was under trouble. This was the greatest missing experiment ever.

The wikipedia article 'Special Relativity' says: Instead of providing insight into the properties of the aether, Michelson and Morley's article in the American Journal of Science reported the measurement to be as small as one-fortieth of the expected displacement but "since the displacement is proportional to the square of the velocity" they concluded that the measured velocity was "probably less than one-sixth" of the expected velocity of the Earth's motion in orbit and "certainly less than one-fourth." Although this small "velocity" was measured, it was considered far too small to be used as evidence of speed relative to the aether, and it was later said to be within the range of an experimental error that would allow the speed to actually be zero. Though Kennedy later also carried out an experiment at Mount Wilson, finding 1/10 the drift measured by Miller, and no seasonal effects, Miller's findings were considered important at the time, and were discussed by Michelson, Lorentz and others at a meeting reported in 1928. There was general agreement that more experimentation was needed to check Miller's results. Lorentz recognised that the results, whatever their cause, did not quite tally with either his or Einstein's versions of special relativity. Einstein was not present at the meeting and felt the results could be dismissed as experimental error. To date, no-one has been able to replicate Miller's results, and modern experimental accuracies are considered to have ruled them out.
Note: Poincare was not mentioned here. Note also the Gruisenick experiment 1, 2, that found differencies, still unconfirmed (Miller-type?). Not mentioned in the modern laser experiments either.

In History of special relativity Poincare was a central name.
Poincare (1895, 1900a) argued that experiments like that of Michelson-Morley show the impossibility of detecting the absolute motion of matter, i.e., the relative motion of matter in relation to the aether. He called this the "principle of relative motion." In the same year he interpreted Lorentz's local time as the result of a synchronization procedure based on light signals.
He assumed that 2 observers A and B, which are moving in the aether, synchronize their clocks by optical signals. Since they believe themselves to be at rest, they must consider only the transmission time of the signals and then cross-reference their observations to examine whether their clocks are synchronous. However, from the point of view of an observer at rest in the aether, the clocks are not synchronous and indicate the local time . But because the moving observers do not know anything about their movement, they do not recognize this. So, contrary to Lorentz, Poincaré-defined local time can be measured and indicated by clocks. Therefore, in his recommendation of Lorentz for the Nobel Prize in 1902, Poincaré argued that Lorentz has convincingly explained the negative outcome of the aether drift experiments by inventing the "diminished time", i.e. that two events at different place could appear as simultaneous, although they are not simultaneous in reality.

This reminds me of the neutrino faster than light - speed. A new paradigm shift too?

The constancy of the speed of light was postulated by Albert Einstein in 1905, motivated by Maxwell's theory of electromagnetism and the lack of evidence for the luminiferous ether but not, contrary to widespread belief, by the null result of the Michelson–Morley experiment. However the null result of the Michelson–Morley experiment helped the notion of the constancy of the speed of light gain widespread and rapid acceptance.

"Test Light Speed in Mile Long Vacuum Tube." Popular Science Monthly, September 1930, p. 17-18.

No Nobel for Relativity.
When Albert Einstein got the Nobel Prize, no mention of relativity was made : The Nobel Prize in Physics 1921 was awarded to Albert Einstein "for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect".

Actually, a Nobel Prize for special relativity (SR) could well have been awarded already in the period 1905-1910. But then, it would have been impossible to ignore the role of Henri Poincaré. Who was against a Nobel Prize including Poincaré? He was not only "a mathematician" ("not a physicist"), as seen by some, but also the first cousin of the French politician Raymond Poincaré, who in 1913 became the President of the French Republic.

Poincare versus Einstein by Roger J Anderton, 2010: Poincare was working on the same ideas as Einstein. Poincare’s theory came before Einstein’s theory, and is a more general theory than Einstein’s theory. There are similarities and differences between Einstein’s SR with Poincare’s theory. Poincare’s theory is just Newtonian physics.
Jaques Fric: “[Poincare] set up all the basic concepts of SR, several years before Einstein did in his the famous paper.

As is well known Einstein did not cite references in his famous paper.

“At least the Relativity principle as well as the method for synchronizing clocks are borrowed from Poincaré published papers (1898-1902). This should explain why Einstein was not awarded the Nobel Prize for the Relativity, but for the photo-electric effect!” i.e. there was dispute over whose theory it was!

The ether, time, speed of light - and invariance.
In 1895 Lorentz suggested that moving bodies should experience a “physical” contraction, compute what it would be in accordance to the Michelson Morley experience and set up a theory on this basis.

Length Contraction (wikipedia): Not only the electrostatic fields, but also the molecular forces are affected in such a way that the dimension of a body in the line of motion is less by the value v² / (2c²) than the dimension perpendicularly to the line of motion. However, an observer co-moving with the earth would not notice this contraction, because all other instruments contract at the same ratio. In 1895 Lorentz proposed three possible explanation for this relative contraction:

• The body contracts in the line of motion and preserves its dimension perpendicularly to it.
• The dimension of the body remains the same in the line of motion, but it expands perpendicularly to it.
• The body contracts in the line of motion, and expands at the same time perpendicularly to it.

Although the possible connection between electrostatic and intermolecular forces was used by Lorentz as a plausibility argument, the contraction hypothesis was soon considered as purely ad hoc. It is also important that this contraction only affected the space between the electron but not the electrons themselves, therefore the name "intermolecular hypotheses" was sometimes used of this effect. The so called Length contraction without expansion perpendicularly to the line of motion and by the precise value (where l₀ is the length at rest in the ether) was given by Larmor in 1897 and by Lorentz in 1904. In the same year Lorentz also argued that also electrons themselves are affected by this contraction. For further development of this concept, see the section Lorentz transformation.

Poincare: “ I am not satisfied with the explanation (physical contraction) of the negative result of the Michelson experiment by the Lorentz theory, I would say that the laws of optics are only depending on the relative motion of the involved bodies”.


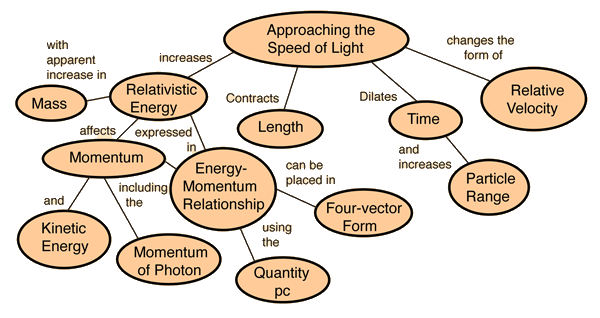
A number of ordinary mechanical quantities take on a different form as the speed approaches the speed of light. At what energies is a particle relativistic? See the equations. The relativistic kinetic energy, the relativistic momentum, the exact expression for pc in terms of kinetic energy, and the photon energy expression E = hc/l = pc when the rest mass energy is negligible compared to the kinetic energy.

Poincaré did not accept the ad hoc "length contraction" hypothesis by FitzGerald and Lorentz. It led to a friendly controversy with Lorentz , mainly about the concept of absolute Space and absolute Time, brought forth by Mach. Poincare emphasised that the Lorentz contraction was just made for adjusting the theory to the experience. Lorentz reported this point of view of Poincaré, in his theory of electromagnetism (1904). “Poincaré has objected to the existing theory of electric and optical phenomena in moving bodies that, in order to explain Michelson’s negative result, the introduction of a new hypothesis has been required, and that the same necessity may occur each time new facts will be brought to light. Surely this course of inventing special hypotheses for each new experimental result is somewhat artificial. It would be more satisfactory if it were possible to show by means of certain assumptions and without neglecting terms of one order of magnitude or another, that many electromagnetic actions are entirely independent of the motion of the system…..”

Can the Lorentz - Fitzgerald Contraction Hypothesis be Real? (2005?).
After rejecting the reality of ether, the relativistic length contraction in SRT was no longer the result of certain forces (real or fictitious), and didn’t need any additional propositions concerning the structure of matter or the nature of the ether. In short, relativistic length contraction became a kinematics effect. The textbook methods for studying the well-known examples in electrodynamics are based on two hypotheses: the Lorentz-Fitzgerald contraction, and the relativistic length contraction. Given that the Lorentz-Fitzgerald contraction was an ad-hoc and theoretically unproven concept, so might the method given in this work be considered which provides some theoretical justification. Thus, regardless of whatever else one may believe about relativistic length contraction, we are led to believe that the Lorentz-Fitzgerald contraction is real.

History of SR: Lange (1885) was the first to coin the expression inertial frame of reference and inertial time scale as operational replacements for absolute space and time, by defining "a reference frame in which a mass point thrown from the same point in three different (non co-planar) directions follows rectilinear paths each time it is thrown is called a inertial frame".

And in 1902, Henri Poincaré published the philosophical and popular-science book "Science and Hypothesis", which included: philosophical assessments on the relativity of space, time, and simultaneity; the opinion that a violation of the Relativity Principle can never be detected; the possible non-existence of the aether but also some arguments supporting the aether; many remarks on non-Euclidean geometry. Poincaré devoted a full chapter to the relativity principle:

“There is no absolute uniform motion, no physical experience can therefore detect any inertial motion (no force felt), there is no absolute time, saying that two events have the same duration is conventional, as well as saying they are simultaneous is purely conventional as they occur in different places.” One can still keep in mind the concept of ether, if it helps for thinking, but it is a unphysical concept, it is a metaphysical concept.

Poincare points out that the “form” of the Lorentz formulae can be demonstrated from the Relativity principle alone, and therefore are implied by this principle alone (with a parameter to specify, related to “c” for the SR), only one hypothesis is required, instead of the local time and the associated three new hypothesis of the article of Lorentz (1904). In The Principles of Mathematical Physics (1904), Poincaré drew some consequences from Lorentz's theory and defined (in modification of Galileo's Relativity Principle and Lorentz's Theorem of Corresponding States) the following principle: "The Principle of Relativity, according to which the laws of physical phenomena must be the same for a stationary observer as for one carried along in a uniform motion of translation, so that we have no means, and can have none, of determining whether or not we are being carried along in such a motion." He also specified his clock synchronization method and explained the possibility of a "new method" or "new mechanics", in which no velocity can surpass that of light for all observers. However, he critically noted that the Relativity Principle, Newton's action and reaction, the Conservation of Mass, and the Conservation of Energy are not fully established and are even threatened by some experiments (prefiguring Noether theorem: 1915).

Cohn illustrated (like Joseph Larmor in the same year) this Lorentz transformation by using rods and clocks: If they are at rest in the aether, they indicate the true length and time, and if they are moving, they indicate contracted and dilated values. Like Poincaré, Cohn defined local time as the time, which is based on the assumption of isotropic propagation of light. Contrary to Lorentz and Poincaré it was noticed by Cohn, that within Lorentz's theory the separation of "real" and "apparent" coordinates is artificial, because no experiment can distinguish between them.

Henri Poincaré (1898) in his paper The Measure of Time drew some important consequences of this process and explained that astronomers, in determining the speed of light, simply assume that light has a constant speed, and that this speed is the same in all directions. Without this postulate it would be impossible to infer the speed of light from astronomical observations, as Rømer did based on observations of the moons of Jupiter. Poincaré also noted that the propagation speed of light can be (and in practice often is) used to define simultaneity between spatially separate events. He concluded by saying, that "The simultaneity of two events, or the order of their succession, the equality of two durations, are to be so defined that the enunciation of the natural laws may be as simple as possible. In other words, all these rules, all these definitions are only the fruit of an unconscious opportunism."

Lorentz argued that there exists only electromagnetic mass, not mechanical mass, and derived the correct expression for longitudinal and transverse mass. And using the electromagnetic momentum, he could explain the negative result of the Trouton-Noble experiment, in which a charged parallel-plate capacitor moving through the aether should orient itself perpendicular to the motion. Also the Experiments of Rayleigh and Brace could be explained. Another important step was the postulate that the Lorentz Transformation has to be valid for non-electrical forces as well.

Wien (1903) recognized an important consequence of the velocity dependence of mass. He argued that superluminal velocities were impossible, because that would require an infinite amount of energy — the same was already noted by Thomson (1893) and Searle (1897). And in June 1904, after he had read Lorentz's 1904 paper, he noticed the same in relation to length contraction, because at superluminal velocities the factor becomes imaginary.


The fringe-shift effect (used today in laser gyroscopes) found in M-M exp. as described in wikipedia SR article. (Note, no mention of Poincare. How could they write about this without mention of his qritique?)
The explanation was found in the FitzGerald–Lorentz contraction, also simply called length contraction. According to this physical law all objects physically contract along the line of motion (originally thought to be relative to the aether), so while the light may indeed transit slower on that arm, it also ends up travelling a shorter distance that exactly cancels out the drift. In 1932 the Kennedy–Thorndike experiment modified the Michelson–Morley experiment by making the path lengths of the split beam unequal, with one arm being very short. In this version a change of the velocity of the earth would still result in a fringe shift except if also the predicted time dilation is correct. Once again, no effect was seen, which they presented as evidence for both length contraction and time dilation, both key effects of relativity.
Einstein derived the FitzGerald–Lorentz contraction from the relativity postulate; thus his description of special relativity was also consistent with the apparently null results of most experiments (though not, as was recognized at the 1928 meeting, with Miller's observed seasonal effects). Today special relativity is generally considered the "solution" to the Michelson–Morley null result. However, this was not universally recognized at the time. As late as 1920, Einstein himself still spoke of a different concept of ether that was not a "ponderable medium" but something of significance nonetheless.

Poincare defines the way to synchronise all the clocks of an inertial frame, by using light signals (1900: La théorie de Lorentz et le principe de réaction, J.Bosscha).

In 1904 at the St Louis conference, he proposes to add the Relativity principle to the five classical “universal” principles of the physics.

At last but not at least, In 1900, he noticed that the recoil of a radiation, of energy E, is m = E/c² [Poincaré, op.cit.t IX p 471] which is nothing else that the famous E = mc². We can see that in 1905 Poincaré, in different articles, had set up all the basic concepts of the special Relativity even though he did not summarize all of them in the framework of a formal theory as Einstein did.

I would like to draw attention to the fact that the Principle of Relativity is part of
Newtonian physics (no, says other). It is only the addition of the idea of constancy of lightspeed that has caused the problems with thinking there is another theory SR different to Newtonian physics.
So working just from the Principle of Relativity without the lightspeed constancy, he is working within the context of Newtonian physics.

Poincaré as a mathematician had a clear formal approach of the Relativity principle. He states first that inertial frames are homogenous allowing to express each coordinate (x,t) of one frame as a linear function of the coordinates of the other frame (x’,t’) and vice versa. He had previously rotated one axis by 180 ° in order to have a full symmetrical situation. This results in four relations with eight unknown parameters. The symmetry of the situation reduces them to four and using relations leaves the equations with only one undetermined parameter, function of the relative speed. The form of this last parameter can be computed taking into account that into a group, by definition, operation by two elements is an element of the group. He never used the statement constancy of lightspeed, though. Just homogenous isotropic and anisotropic space!

Enrico Giannetto The rise of Special Relativity: Henri Poincaré’s works before Einstein, 1998: Without the absurd "length contraction" hypothesis, the Michelson-Morley experiment UNEQUIVOCALLY confirms the equation c'=c+v given by Newton's emission theory of light and showing how the speed of light varies with v, the speed of the emitter relative to the observer, and refutes the assumption that the speed of light is independent of the speed of the light source (Einstein's 1905 light postulate).

Poincares Model.
Back to Poincare's math:

x'=(x-Vt) (1-V²/K)^-1/2 ; y'=y ; z'=z

t'=[(t-(Vx/K)] (1-V²/K)^-1/2

V is the relative velocity of the two frames and K is a parameter having the dimension of a square of a speed which, is the maximum possible value of V (to keep the equation real) . Whether K = c², we recognize the Lorentz equations, whether K = infinity, it is Newton.

The interesting thing is that each value of K (continuous parameter) defines a continuous family (with a group structure) of inertial frames.

Poincaré understood that such Relativity principle reflects symmetry properties of the physical laws: invariance of physical laws under a group of transformations: the Poincaré group, including three spatial rotations, three hyperbolic rotations (boosts) and four translations, conferring to the Minkowski space (SR spacetime), the maximum possible number of symmetries : n( n+1)/2 = 10.

For d−1∈ℕ, d-dimensional Minkowski space is the Lorentzian manifold whose underlying smooth manifold is the Cartesian space ℝ d and whose pseudo-Riemannian metric is at each point the Minkowski metric. This is naturally a spacetime.
Theorem. Minkowski spacetimes is a stable? solution of the vacuum Einstein equations.
Reissner-Nordström spacetime is a generalization? What are called Einstein’s equations are the equations of motion of gravity: the Euler-Lagrange equations induced by the Einstein-Hilbert action. Einstein's vacuum fi eld equation, in analogy with Laplace vacuum field formulation of Newtonian theory can be formulated as the statement that the trace of the relativistic analogue of wave is zero. Compare to the knots again. In Synthetic Differential Geometry (SDG), the reals R have the structure of a (non-trivial) ring, not a field, and the main axiom states one of the basic insights, namely, that \in the in finitely small, every curve is a line in a unique way." This gives hidden dimensions (in 26D model) and curvature that doesn't obey ordinary laws at quantum level (in TGD). The c.c.

Gonzalo Reyes, A derivation of Einstein’s vacuum field equations (pdf)
J.K. Webb et al. 2010: Indications of a Spatial Variation of the Fine Structure Constant

He showed that the transformations are a consequence of the Principle of Least Action and developed the properties of the Poincaré stresses. He demonstrated in more detail the group characteristics of the transformation, which he called the Lorentz group, and he showed that the combination is invariant. While elaborating his gravitational theory, he said the Lorentz transformation is merely a rotation in four-dimensional space about the origin, by introducing as a fourth imaginary coordinate.

The theory of Lorentz and the principle of reaction (1900)

Compare to the knot theory where the result also is invariant, only the path varies.

Poincare group, ISO(p,1) is the isometry group of Minkowski spacetime of dimension d+1: the group of affine transformations on ℝ 4 which preserve the Minkowski "metric". The norm of Minkowski is quadratic. The group elements are multiplied by composing maps. The Poincaré group G may also be described as a semidirect product (ℝ⊕ℝ 3)⋊O(1,3) where O(1,3), the Lorentz group, consists of all linear transformations L:ℝ 4→ℝ 4 that preserve the Minkowski inner product of signature (1,3). The Lorentz group is a 6-dimensional Lie group. It has four connected components.

This is obviously, the modern approach. Time is the 'dragging' i-factor (ether?)?

Einstein, more intuitive and sticking to physical principles, first states the two postulates: Relativity principle (borrowed to Poincaré) and constancy of light speed in all Galilean frames. Then he studies the methods for synchronizing clocks in a frame ( borrowed to Poincaré) , allowing also to define space milestones ( with the help of the constant light speed).

Then, after defining exactly the terminology, he considers a moving frame and writes the relations between the coordinates of the two frames by considering the clock synchronisation equation in the two different frames derived from the light speed constancy. The paper of Einstein is a more extensive treaty about Relativity, as in addition to the demonstration of the Lorentz formula, he considers also the cinematic, and the dynamic of the electron, it is a first synthesis about the theory of special relativity and its implications. ( E = mc² will come later in a second paper).

So, why is the work of Poincaré in Special Relativity so ignored ?
Poincaré did not realize the revolution implied by this new theory, as he had many others topics of interest especially in mathematics. His formal (maybe too speculative) approach did not reflect the “physical reality” implied by the theory. His position on the ether remains quite ambiguous, as he did not reject definitely the concept as Einstein did (at the beginning, as later Einstein had a more ambiguous position too, ether being a “hard to kill “concept). In some following papers, he expresses some doubts about the universality of the Relativity principle. In addition, he never published a so extensive treaty as Einstein, whose approach was more physical, more practical, closer to the physical reality [for that time]...

Poincare was shy. He let other become famous in his place, as Fuchs, Lorentz, maybe Einstein...
Einstein was young, bold, unknown at that time, and therefore took over the whole thing.

Einstein has always denied to have known Poincaré publications. It’s hard to believe as his friends Maurice Solovine and Carl Seelig, report Einstein had read the Poincaré book “La Science et l'hypothèse” (no absolute time, no absolute space, no ether ... ) around 1902-1904. This book was commented at their reading commitee « Académie Olympia » during several weeks (ref. 8, pages 129 et 139 ; ref. 9, page VIII and ref. 17, page 30). His position at the Swiss office patent in charge of “electromagnetism” implied that part of his job was to read and summarize the main publications on this topic (he summarized several papers from the French “Academie des sciences”).

At the end of his life, Einstein wrote in 1955 in a letter to Carl Seelig: «There is no doubt, if we look back to the development of the Relativity theory, special Relativity was about to be discovered in 1905. Lorentz already noticed that the transformations (named Lorentz transformations) were essential in the Maxwell theory and Poincaré had gone even further. At that time I only knew Lorentz work of 1895, but I knew neither Lorentz nor Poincaré further work. This why I can say that my work of 1905 was independent » (ref 8, page 11).

Anyway, Einstein had a different approach, he popularised the Special Relativity, and developed “ alone” the General Relativity ( even though Hilbert derived the field equation of GR a few days before Einstein, but by using Einstein work so the equation was rightly attributed to Einstein) .

When the Nobel Committee decided to award Einstein the price, Lorentz, who was a member, objected that it was Poincaré who had found the full group of transformations of the SR, and it would be unfair not to associate him. But as Poincaré was dead at that time, Einstein was awarded the Nobel price for his work on the photo electric effect: That’s diplomacy…

Poincare and gravity.
Pentcho Valev: Look at the formulae used by Poincaré in his articles : Poincaré had already formulated special relativity before Einstein, and was already considering the possibility to extend it to gravity (where Einstein was struck for the rest of his life). There had also been the contribution by Lorentz - precisely the relativity principle that Poincaré formulated as early as 1895.

H. Poincaré appreciated Einstein's efforts on explaining popularly the principle of relativity but he called it a "mechanics of Lorentz'" because it was H.Lorentz who, step by step, was approaching this new physical description basing on experimental data. In addition, apart from playing with (x,t), there were equations of motion with severe problems (self-action, radiation resistance) not resolved even today.

Poincaré supported 1905 the Lorentz transformation against an alternative theory by Langevin. He also pointed out that the gravitational interaction had to travel at the speed of light, and even spoke about "gravitational waves". Perhaps people around Langevin did not like Poincaré's attitude. In any case, he was forced to send to the Circolo Matematico di Palermo his long paper "Sur la dynamique de l'électron", and this delayed its publication.

On the Dynamics of the Electron (1906)
Mayeul Arminjon: Lorentz-Poincaré relativity and a scalar theory of gravitation (2007?)

Poincaré's version of the relativity principle was different from Einstein's (1905), indeed Poincaré's version (1904) was this: "The laws of physical phenomenons must be the same, whether for a fixed observer, as also for one dragged in a motion of uniform translation, so that we do not and cannot have any mean to discern whether or not we are dragged in a such motion." This formulation does not preclude in any way the possibility that there might be an absolute meaning to the words "fixed" and "moving". In essential features the Poincare model gives SR too, proved by many.

Today this motion is interpreted as 70% dark energy in our universe, because of the ever increasing acceleration, oddly without ceasing energy from the vacuum.

Apart from the historical aspect, it is important for physics research to realize that the physics of special relativity was found by scientists who based their work on the concept of ether. Indeed today's physics makes it obvious that vacuum has physical properties.

Loops, knots, strings,..

Knots are ubiquitous: We encounter them in woven materials, in the numerous sailors’ knots, and in constantly entangled electric cables and extension cords. When putting on their shoes, even small children learn to master their first knots – long before they can read and write. Even our DNA can be complicatedly knotted. From a mathematical point of view, knots that seem completely different at first sight can belong to the same class. The essential criterion is that one knot can be transformed into another by means of simple deformations. The most simple example is a rubber band. Topologically speaking, every shape you can create from it without cutting open the loop and joining it back together is equivalent to the initial rubber band. A completely different knot, for example, is the trefoil knot (see figure 1). This knot cannot easily be tied from an intact rubber band. Furthermore, several interlocked loops can constitute even more complex structures.

TGD can much be seen as a Universe of knots, loops or bubbles. See Knots in TGD. Also E. Witten. Fivebranes and Knots.

Knots can now be tied systematically in the microscopic world. A team at the Max Planck Institute for Dynamics and Self-Organization in Gottingen (Germany) since September 2010, has now found a way to create every imaginable knot inside a liquid crystal. Starting points of the new method are tiny silica microspheres confined in thin liquid crystal layers. Surrounding these microspheres, a net of fine lines is formed where the molecular orientation of the liquid crystal is altered. The researchers discovered a method to twist and link these lines in such a manner as to create every knot imaginable.

A single silica microsphere entering the layer changes the surrounding alignment substantially: around the sphere a ring-shaped region forms in which no preferred direction can be discerned. Scientists refer to such disruptions in the molecular order as defect lines. Since the defect ring surrounding a microsphere reflects light differently than the rest of the liquid crystal, it can be easily detected. "It looks as if every microsphere were surrounded by its own ring – similar to the planet Saturn", explains Tkalec . These Saturn’s rings are oriented perpendicularly to the average orientation of molecules between the glass plates.

Creating knots requires the defect rings of neighbouring microspheres to be able to attach to each other in two directions. In order to achieve this, the scientists used a "trick": if the upper plate confining the liquid crystal layer is turned by 90 degrees, the alignment of the molecules is changed. While the lower molecules still point in the same direction as before, the upper ones are also rotated by 90 degrees. In between, the transition is gradual. Scientists refer to this as a twisted or chiral nematic liquid crystal. "In this experimental set-up, the defect rings surrounding the spheres are slightly buckled - like a buckled wheel of a bicycle".

Uroš Tkalec, Miha Ravnik, Simon Čopar, Slobodan Žumer und Igor Muševič, Reconfigurable Knots and Links in Chiral Nematic Colloids, Science, 1 July 2011. http://www.science … /62.abstract

Tying knots and linking microscopic loops of polymers, macromolecules, or defect lines in complex materials is a challenging task for material scientists. We demonstrate the knotting of microscopic topological defect lines in chiral nematic liquid-crystal colloids into knots and links of arbitrary complexity by using laser tweezers as a micromanipulation tool. All knots and links with up to six crossings, including the Hopf link, the Star of David, and the Borromean rings, are demonstrated, stabilizing colloidal particles into an unusual soft matter. The knots in chiral nematic colloids are classified by the quantized self-linking number, a direct measure of the geometric, or Berry’s, phase. Forming arbitrary microscopic knots and links in chiral nematic colloids is a demonstration of how relevant the topology can be for the material engineering of soft matter.

Provided by Max-Planck-Gesellschaft (news : web)

A revolution in knot theory,
Figure 1. This knot has Gauss code O1U2O3U1O2U3. Graphic by Sam Nelson. As Nelson reports, mathematicians have devised various ways to represent the information contained in knot diagrams. One example is the Gauss code, which is a sequence of letters and numbers wherein each crossing in the knot is assigned a number and the letter O or U, depending on whether the crossing goes over or under.

In his article “The Combinatorial Revolution in Knot Theory”, to appear in the December 2011 issue of the Notices of the AMS, Sam Nelson describes a novel approach to knot theory that has gained currency in the past several years and the mysterious new knot-like objects discovered in the process.

Knot theory is usually understood to be the study of embeddings of topological spaces in other topological spaces. Classical knot theory, in particular, is concerned with the ways in which a circle or a disjoint union of circles can be embedded in R3. Knots are usually described via knot diagrams, projections of the knot onto a plane with breaks at crossing points to indicate which strand passes over and which passes under, as in Figure 1. However, much as the concept of “numbers” has evolved over time from its original meaning of cardinalities of finite sets to include ratios, equivalence classes of rational Cauchy sequences, roots of polynomials, and more, the classical concept of “knots” has recently undergone its own evolutionary generalization. Instead of thinking of knots topologically as ambient isotopy classes of embedded circles or geometrically as simple closed curves in R3, a new approach defines knots combinatorially as equivalence classes of knot diagrams under an equivalence relation determined by certain diagrammatic moves. No longer merelysymbols standing in for topological or geometric objects, the knot diagrams themselves have become mathematical objects of interest.
Identifying knot invariants (functions used to distinguish different knot types) by checking invariance under the moves has been common ever since. A recent shift toward taking the combinatorial approach more seriously, however, has led to the discovery of new types of generalized knots and links that do not correspond to simple closed curves in R3.

Like the complex numbers arising from missing roots of real polynomials, the new generalized knot types appear as abstract solutions in knot equations that have no solutions among the classical geometric knots. Although they seem esoteric at first, these generalized knots turn out to have interpretations such as knotted circles or graphs in three-manifolds other than R3, circuit diagrams, and operators in exotic algebras. Moreover, classical knot theory emerges as a special case of the new generalized knot theory. This diagram-based combinatorial approach to knot theory has revived interest in a related approach to algebraic knot invariants, applying techniques from universal algebra to turn the combinatorial structures into algebraic ones. The resulting algebraic objects,with names such as kei, quandles, racks, and biquandles, yield new invariants of both classical and generalized knots and provide new insights into old invariants. Much like groups arising from symmetries of geometric objects, these knot-inspired algebraic structures have connections to vector spaces, groups, Lie groups, Hopf algebras, and other mathematical structures.

In the 19th century, Lord Kelvin made the inspired guess that elements are knots in the “ether”. Hydrogen would be one kind of knot, oxygen a different kind of knot—and so forth throughout the periodic table of elements. This idea led Peter Guthrie Tait to prepare meticulous and quite beautiful tables of knots, in an effort to elucidate when two knots are truly different. From the point of view of physics, Kelvin and Tait were on the wrong track: the atomic viewpoint soon made the theory of ether obsolete. But from the mathematical viewpoint, a gold mine had been discovered: The branch of mathematics now known as “knot theory” has been burgeoning ever since.

The scientists, Gina Passante, et al., from the University of Waterloo in Ontario, Canada, have presented their experimental results for the quantum solution of the approximation of the Jones polynomial, which is a knot invariant. By approximating the Jones polynomial, researchers can determine whether two knots are different. Making this distinction is a fundamental problem in knot theory, and has applications in statistical mechanics, quantum field theory, and quantum gravity. Although approximation of the Jones polynomial is a classical problem that is very difficult to solve, the results show that the problem can be solved using a “one quantum bit model.”

As the researchers explain, the DQC1 algorithm extracts the power of one bit of quantum information alongside a register of several qubits.

“The ‘one quantum bit model’ means that there is one initialized qubit in the experiment, meaning that we can only control the initial state of one qubit,” Passante told. “For four qubits, the other three qubits are initially in a completely random state.”

The scientists experimentally implemented the algorithm using a liquid state nuclear magnetic resonance (NMR) quantum information processor. They implemented the model with the molecule transcrotonic acid, with its four carbon nuclei representing the algorithm’s four qubits. Then the researchers generated radio frequency pulses, starting randomly and improving through iterations.

“Successful experimental implementation of this algorithm relies on our ability to manipulate the qubits to perform the unitary transformations,” Passante said. “These manipulations must be done very accurately and quickly in order to get a reliable result, since the quantum states are very fragile.”

In simulations, the researchers found that, in the case of knots whose braid representations have four strands and three crossings, the algorithm could identify distinct knots 91% of the time.

Figure 2. The molecule transcrotonic acid was used in the quantum algorithm DQC1. The molecule’s four carbon nuclei represent the algorithm’s four qubits, only one of which is initially controlled. The algorithm can solve the Jones polynomial, a difficult classical problem that involves distinguishing different knots. Image copyright: G. Passante, et al. The study is published in a recent issue of Physical Review Letters. (From Phys.org.)
G. Passante, O. Moussa, C.A. Ryan, and R. Laflamme. “Experimental Approximation of the Jones Polynomial with One Quantum Bit.” Physical Review Letters 103, 250501 (2009)

As sailors have long known, many different kinds of knots are possible; in fact, the variety is infinite. A *mathematical* knot can be imagined as a knotted circle: Think of a pretzel, which is a knotted circle of dough, or a rubber band, which is the “un-knot” because it is not knotted. Mathematicians study the patterns, symmetries, and asymmetries in knots and develop methods for distinguishing when two knots are truly different.

Mathematically, one thinks of the string out of which a knot is formed as being a one-dimensional object, and the knot itself lives in three-dimensional space. Drawings of knots, like the ones done by Tait, are projections of the knot onto a two-dimensional plane. In such drawings, it is customary to draw over-and-under crossings of the string as broken and unbroken lines. If three or more strands of the knot are on top of each other at single point, we can move the strands slightly without changing the knot so that every point on the plane sits below at most two strands of the knot. A planar knot diagram is a picture of a knot, drawn in a two-dimensional plane, in which every point of the diagram represents at most two points in the knot. Planar knot diagrams have long been used in mathematics as a way to represent and study knots.

In the mid-1990s, mathematicians discovered something strange. There are Gauss codes for which it is impossible to draw planar knot diagrams but which nevertheless behave like knots in certain ways. In particular, those codes, which Nelson calls *nonplanar Gauss codes*, work perfectly well in certain formulas that are used to investigate properties of knots. Nelson writes: “A planar Gauss code always describes a [knot] in three-space; what kind of thing could a nonplanar Gauss code be describing?” As it turns out, there are “virtual knots” that have legitimate Gauss codes but do not correspond to knots in three-dimensional space. These virtual knots can be investigated by applying combinatorial techniques to knot diagrams.

Just as new horizons opened when people dared to consider what would happen if -1 had a square root—and thereby discovered complex numbers, which have since been thoroughly explored by mathematicians and have become ubiquitous in physics and engineering—mathematicians are finding that the equations they used to investigate regular knots give rise to a whole universe of “generalized knots” that have their own peculiar qualities. Although they seem esoteric at first, these generalized knots turn out to have interpretations as familiar objects in mathematics. “Moreover,” Nelson writes, “classical knot theory emerges as a special case of the new generalized knot theory.”

All colorings of the trefoil knot by the three-element kei R3 with operation table given by The matrix
. 1 2 3
_ |____
1 |1 3 2
2 |3 2 1
3 |2 1 3.

The finiteness condition for coloring objects is not required; if the target kei is infinite but has a topology, for instance, then the set of homomorphisms itself is a topological space whose topological properties then become knot invariants. Counting invariants are only the beginning; any invariant of algebraically labeled knot diagrams defines an enhancement of the counting invariant by taking the multiset of invariant values over the set of colorings of the knot.

Figure 3. Kei colorings of the trefoil by R3. Counting invariant 9 with respect to R3 and enhanced invariant p(t) = 3t +6t3. A more sophisticated example of an enhancement is the family of CJKLS quandle cocycle invariants which associate a Boltzmann weight (f ) with each quandle coloring f , determined by a cocycle in the second cohomology of T. In true combinatorial-revolutionary spirit, such two-cocycles have a geometric interpretation as virtual link diagrams.

More information: Related to this subject are an upcoming issue of the Journal of Knot Theory and its Ramifications, devoted to virtual knot theory, and the upcoming Knots in Washington conference at George Washington University, December 2-4, 2011, which will focus on on “Categorification of Knots, Algebras, and Quandles; Quantum Computing”.
Provided by American Mathematical Society
http://www.physorg.com

Figure.4. For every knot (left) an equivalent interpretation with the help silica microspheres can be found (centre). The right image shows the real experimental result. © AAAS / Science

In the theoretical part of their study they showed that for every conceivable knot a mathematically equivalent knot can be found which can be implemented in this way. "With the help of microspheres in a chiral nematic liquid crystal, we can create practically every knot that you can imagine", says Tkalec. The researchers now hope that these findings will help to better understand the complex knotting of DNA. "The knotting of DNA molecules, for example, plays an important role in many vital processes such as replication or transcription of DNA", says Uroš Tkalec. In 2006 he wrote: Colloids inducing quadrupolar order crystallize into weakly bound two-dimensional ordered structure, where the particle interaction is mediated by the sharing of localized topological defects. Colloids inducing dipolar order are strongly bound into antiferroelectric-like two-dimensional crystallites of dipolar colloidal chains. Self-assembly by topological defects could be applied to other systems with similar symmetry.

Quadrupolar order is important in DNA's.

The hadronic/mesonic strings in TGD, and how they code for the upcoming dimensions and color? Also the CP2 sheets? The scalar fundamental unity, also behind all kinds of numbers? I come back to this. Primes are open ended. But are they linked to knots too? Then this could be a hadronic string?