Contemporary physicists and even philosophers often understood Einstein’s work as a science of signals with implications for telecommunication technologies. Descriptions of Einstein’s work as a study of light signals abounded during the period of its emergence. The philosopher and mathematician Alfred North Whitehead, one of the most important thinkers to challenge the theory, called it both “signal-theory” and “message theory.”
Einstein was also a founding father of quantum physics and the discovery of radioactivity and the atomic bombs. At his death, he was disillusioned with quantum mechanics, but further applications and experiments led to its becoming the basis of our modern understanding of the Universe. This is as important as the relativity, but here we stick to gravity and relativity.
Albert Einstein presented the theories of Special Relativity and General Relativity in groundbreaking publications that either contained no formal references to previous literature, or referred only to a small number of his predecessors for fundamental results on which he based his theories, most notably to the work of Hendrik Lorentz for special relativity, and to the work of Gauss, Riemann, and Mach for general relativity. See History of special relativity and History of general relativity.
Under the photon theory of light, after Einstein, a photon is a discrete bundle (or quantum) of electromagnetic (or light) energy. Electromagnetic radiation = light, is a special case of transverse wave in that there is no medium undergoing transverse oscillations, as in the case of a string. A center of action made up of 'nothing' but transmitting energy is hard to understand. Instead they say, radiation is the result of electric and magnetic fields simultaneously propagating in empty space. For a long time, physicists were of the view that light was a wave or field - and similar to all the other waves seen in nature, with a string at the center - and electromagnetic waves, or radiation in short, was also the result of the oscillations of an underlying medium, which was called the ether.
We shall look at this lightray, so different from all other waves, later.
An independence of the velocity of light of that of the source compared to inertia, seen as resistence of matter against change. Light bought tension and imbedding of space. But only a part of the imbeddings. There are other rays too, as X-rays, gammarays, cosmic strings etc. lightlike massless extremals.
In What is wrong with relativity?
Einstein could sometimes speak as though the aether was superfluous (Einstein 1905) and at other times say "space without aether is unthinkable" (Einstein 1922). This was due, of course, to not starting with physical terms—matter its motion, and its interactions (force). A physical theory which included radiation would have to start by stating whether an aether, action-at-a-distance, or ballistic transmission of force was being postulated It explains, also, how mass and inertial force get into the special theory which is founded on a geometrization of uniform velocities, for it is well known that inertial forces do not appear when the velocities are uniform. Formulae which purport to give the relation between measurements in one state of uniform velocity and those made in another state of uniform motion cannot logically throw any light on what happens during the change from one state to the other. This is only possible by using the cuckoo process—assuming Newton's second law and the conservation of momentum, and then modifying them.See. the clock paradox, twin paradox, time dilation etc. Einstein was not satisfied with the relativity theory of Poincaré and Lorentz which stopped short of including accelerating systems, thus still leaving something apparently 'absolute'. Einstein was seen as the 'Mad Dictator' rushing around at deadly pace, who saw that acceleration produces forces (inertial) whereas uniform velocity does not. Einstein was led to assert that these forces cannot be distinguished from ordinary gravitational force. Still Einsteins Universe is static today.
Natural laws must be expressed by equations which are covariant under a group of continuous coordinate transformations. This group, which Einstein took as the algebraic expression of a general principle of relativity, included, as a subgroup, the Lorentz transformations which Poincaré had taken as the algebraic expression of the restricted principle. The principle of covariance— the laws of physics must be expressed in a form independent of the coordinate system, and the mathematical development of this condition - which Einstein did with Grossman et al. The proposal to describe gravity by means of a pseudo-Riemannian metric was first made by Einstein and Grossmann in the so called Entwurf theory published 1913. This was followed by several attempts of Einstein to find valid field equations for this theory of gravity. Hilbert and Klein had the solution.
Instant action and absolute space.
The leading theory of gravitation in 1905 was Newton's, based on instantaneous action at a distance. When Poincaré sought to bring gravitational attraction within the principle of relativity, he saw it had to propagate with a velocity no greater than that of light in empty space. Speed of light was the clue, which turned the interest to how it was propagated in empty space. The ether was not as important as light was as a signal, giving GR.
The characteristic feature of Galileo's spacetime was the set of horizontal slices representing "planes of simultaneity". On a given plane, all of its events are simultaneous. This is the notion of Absolute Time, in which all observers agree on the elapsed-time between two given events. In the particular case of "zero elapsed-time", all observers agree that the events on a given horizontal plane are simultaneous.
A sphere in an otherwise empty Universe could not be conceived to rotate, and a pair of spheres could be conceived to rotate relative to one another, but not to rotate about their center of gravity. A more recent form of these objections was made by Mach. Mach's principle proposes that mechanics is entirely about relative motion of bodies and, in particular, mass is an expression of such relative motion. So, for example, a single particle in a Universe with no other bodies would have zero mass (no motion). According to Mach, Newton's examples simply illustrate relative rotation of spheres and the bulk of the Universe. This twist was the same as between Newton (absolutist) and Leibniz (relativist) much earlier, and was only renewed. And between Einstein, Podolsky, Rosen (=EPR), Bohr and Bohm (later about the EPR-paradox). Today the ether discussion is back in form of vacuum, dark energy, quintessence or Grid.
When, accordingly, we say that a body preserves unchanged its direction and velocity in space, our assertion is nothing more or less than an abbreviated reference to the entire universe. —Ernst Mach
Two bodies orbiting around a common barycenter. Supposing the bodies tied by a rope to hold them together (rather than gravity, which is ignored in this example), the rope is under tension if the bodies are rotating relative to absolute space (according to Newton), or because they rotate relative to the Universe itself (according to Mach), or because they rotate relative to an inertial frame of reference according to modern ideas.
According how the letter for speed became c and not V here.
Einstein's extension of the Principle of Relativity to all physical laws requires us to abandon Galileo's Spacetime - in particular, its universal "planes of simultaneity" - that is, the notion of Absolute Time.
But we must also note that we still cannot explain time nor gravity well. 'Planes of simultaneity' (nonlocality?) may still be there at work, seen in the "action at a distance" in quantum mechanics, as instance.
Relativity: The special and general theoryEinsteins light - the most wonderful thing in the world.
Einstein, Albert (1916), "Die Grundlage der allgemeinen Relativitätstheorie" (PDF), Annalen der Physik 49,
NMJ Woodhouse (2003). Special relativity. London: Springer.
Rafael Ferraro (2007). Einstein's Space-Time: An Introduction to Special and General Relativity. Easy text. Good as a start.
Space and Time: Inertial Frames (Stanford Encyclopedia of Philosophy)
In 1907, Einstein explained to a colleague that relativity theory was concerned with communication signaling — and not with other types of signs or signals:
I now designate the kind of velocity that, according to the theory of relativity, cannot be greater than the velocity of light in a vacuum as “signal velocity.” This is a velocity which a one-time (not regularly recurring) influence, which is not yet determined by past electrodynamic processes, is propagated; thus, we are dealing here with the propagation of an influence that could, for example, be used for sending an arbitrary signal. The propagation velocity…in your analysis refers to a periodical process (periodical amplitude change, not an amplitude change of the most general kind.)Einstein's description of the Michelson-Morley experiment illustrated just how heavily he relied on theories of communication, while he nonetheless effaced these constitutive connections to communications technology. He went as far as describing the Michelson-Morley experiment as a telecommunication machine, that is, as an experiment about the speed of “signals.”
From that time onward Einstein’s notion of signal was one which could be “arbitrary” and “one-time (not regularly recurring)” of “the most general kind” and which was “not yet determined by past…processes.” His work was concerned with a particular form of measurement—one which differed significantly from most micrometrical measurement techniques employed during the previous century - the departure and arrival of signals. Whitehead understood that the most important conclusions of relativity arose because light “was our quickest system of signals.” Yet, he argued that a “system of signals” should not be elevated to a theory of the universe. In contrast to Einstein, Whitehead stressed the connections of relativity to current technical limitations for signaling... Einstein started his argument by insisting that the constancy of the speed of light was a universal fact of nature; Whitehead started his by noting that it was, to that day, the quickest way of sending signals. In doing so, he placed the contemporary reality of telecommunication technologies of his era at the origin of our relativistic understanding of time.
De Broglie framed Einstein’s contribution as proving the “absence of signals which travel at infinite speed” and realizing “the fact that no signal can travel with a speed greater than that of light in a void.” The world described by Einstein was the way it was because “signaling is only possible” in certain conditions and not in others.
Einstein became acutely concerned (personally and professionally) with communications media, and, in particular, with their speed. Could love (to Elsa) be sent through the mail, wondered he. Today we use the internet. The expansion of electromagnetic communication technologies with wireless communication and radar, and their reach into everyday life occurred in exact parallel to the expansion and success of Einstein’s theory of relativity. He claimed himself that Michelson-Morley was not so important for his theory.
Until 1903 most wireless applications were still military. In 1905, when Einstein published his famous paper, wireless transmission could only be used for the transmission of simple signals to a few highly specific places. Long-distance communications were mostly carried out through the post, although telegraph networks continued to expand. In 1907, a decade after the Bell telephone patents expired, Einstein could telephone some of his friends. Wireless transfer of voice occurred experimentally a few years later. WWI boosted this evolution very much. Radio came after 1920. I remember myself when we got the first television on the 60's, what a miracle!
In Einstein’s universe all actions had to be carried by a signal. He forcefully criticized Newton’s theory because of its reliance on the concept of “action at a distance,” a phrase that increasingly referred to Newton’s uncritical notion of bodies (such as planets) acting on each other without offering any explanation for how actions were actually carried from one body to the other. How, Einstein argued instead, were these forces transmitted exactly and at what speed? In “Einstein’s theory,” explained Lorentz, “gravitation itself does not spread instantaneously, but with a velocity…that may be compared to that of light.”
One of the most revolutionary assertions of Einstein was that the universe was essentially curved. The idea that the shortest path between two points was not, as in Euclidean geometry, a straight line was directly connected to the universe’s curved shape. How could a curve be the shortest path between two points? If the shortest path was defined as that travelled by an electromagnetic signal in the presence of a gravitational field, the result was indeed a curve.
Einstein and many of his interlocutors defined the relation between cause and effect in terms of signaling. The pulling of the string and the ringing of the bell were not simultaneous: “causality, whatever its nature, cannot propagate itself with a velocity greater than that of light."
But when Einstein turned to the study of moving vehicles to expand his theory of relativity from a special to a general case, the rules for understanding the movement of these vehicles were radically different than they had been before the advent of competing electromagnetic forms of communication. The post-post epoch was characterized instead by field physics that contrasted with previous action-at-a-distance theories of the universe and of gravitation/acceleration.
Who invented relativity?
The “theory of relativity” today, usually means the work of Albert Einstein. These ideas are distinguished from previous theories not by relativity itself, but by the way in which relativistically equivalent coordinate systems are related to each other. Almost every idea and formula of the theory had been anticipated by others.
For example, Lorentz covariance and the inertia of energy were both (arguably) implicit in Maxwell’s equations. Also, Voigt formally derived the Lorentz transformations in 1887 based on general considerations of the wave equation*. In the context of electro-dynamics, Fitzgerald, Larmor, and Lorentz had all, by the 1890s, arrived at the Lorentz transformations, including all the peculiar "time dilation" and "length contraction" effects (with respect to the transformed coordinates) associated with Einstein's special relativity. By 1905, Poincare had clearly articulated the principle of relativity and many of its consequences, had pointed out the lack of empirical basis for absolute simultaneity, had challenged the ontological significance of the ether, and had even demonstrated that the Lorentz transformations constitute a group in the same sense as do Galilean transformations. In addition, the crucial formal synthesis of space and time into spacetime was arguably the contribution of Minkowski in 1907, and the dynamics of special relativity were first given in modern form by Lewis and Tolman in 1909. Likewise, the Riemann curvature and Ricci tensors for n-dimensional manifolds, the tensor formalism itself, and even the crucial Bianchi identities, were all known prior to Einstein’s development of GR in 1915. In view of this, is it correct to regard Einstein as the sole originator of modern relativity?*In Voigt's theory the speed of light is invariant, but his transformations mix up a relativistic boost together with a rescaling of space-time. Maxwell's electrodynamics is both scale invariant and Lorentz invariant, so the combination is invariant too. But scale transformations are not a symmetry of all the laws of nature, only of electromagnetism, so these transformations cannot be used to formulate a principle of relativity in general. From History of Lorentz transformations. Lorentz later developed an Ether theory where the ether is completely motionless, and the speed of light in the aether is constant in all directions. He used varying time for his calculations for moving systems, as Einstein in his famous train-thought exp.. The experimental measurement of time dilation by Ives and Stillwell (1938) and others settled the issue in favor of the Lorentz transformation.
Wilhelm Wein proposed that the Nobel prize of 1912 be awarded jointly to Lorentz and Einstein. "While Lorentz must be considered as the first to have found the mathematical content of relativity, Einstein succeeded in reducing it to a simple principle. One should therefore assess the merits of both investigators as being comparable."
In 'A Note on Relativity Before Einstein':
'Relativity before Einstein' made no mention of the work of Joseph Larmor, whose early derivation of the Lorentz transformation seems to be less well known than those of Lorentz and Poincare. In 1897, Larmor, starting from a first-order transformation similar to Lorentz's first order version, presented the correct form of what is now known as the Lorentz transformation. In his presentation of the theory in 1900 Larmor saw the time dilation effect as a consequence of Maxwell's electromagnetic theory. It was Lorentz who, in 1895, introduced the notion of the relativity of simultaneity (local time), without the time dilation effect. Poincare in 1900 discussed how Lorentz's local time would arise from the procedure of synchronizing moving clocks by exchanging light signals assumed to travel at the same speed in either direction. Lorentz presented the correct version of the transformation in 1899, and discussed the variation of mass with velocity arising from it. In 1902 Lorentz was aware of Larmor's 1897 work but apparently missed its significance. Nevertheless, the credit for the first presentation of the Lorentz transformation including the crucial time dilation belongs to Larmor.Is there anything absolute (universal)? It seems as if we've gotten rid of everything that has to do with universal notions of time and universal notions of space. Our spacetime model can no longer have these once-universally accepted lines and planes. What The Principle of Relativity has done is to make the Light Cone absolute.
experiments like that of Michelson-Morley show that it seems to be impossible to detect the absolute motion of matter or the relative motion of matter in relation to the ether. And although most physicists had other views, Poincaré in 1900 stood to his opinion and alternately used the expressions "principle of relative motion" and "relativity of space". He criticized Lorentz by saying, that it would be better to create a more fundamental theory, which explains the absence of any ether drift, than to create one hypothesis after the other.In What I Never Realized About Relativity - about ether.
Most popular science accounts and even text-books on the SR start by describing the Michelson-Morley experiment, which leaves the impression that it played a decisive role in the development of relativity by Einstein. Some books like Kleppner/Kolenkow mention that it probably was of no great significance but fail to mention exactly what experiments, if any led Einstein to relativity.
"An Introduction to Special Relativity" by Robert Resnick describes two experiments that Einstein himself says played a part in the development of relativity - stellar aberration and Fizeau's observation of the dragging of light by moving water (first predicted by Fresnel). The book treats relativistic kinematics, relativistic dynamics, and relativity and electromagnetism and contains special appendices on the geometric representation of space-time and on general relativity.
What is striking about these two experiments is that none of them, in a very clear-cut way, lead to the idea that the ether was a figment of the physicists' imagination. At least, they're not as unambiguous in their conclusions as the Michelson-Morley experiment. Einstein said in an interview, in his later life, that he wasn't quite sure if he knew much about Michelson-Morley when he discovered relativity. He says that at most, he might have been aware of the negative result, but not the actual details. This seems to be the correct version, as he admits having read a book by Lorentz, which mentioned it.
The real origin of relativity, then, mostly lies in a thought experiment Einstein had when he was 16 - about what he would see if he ran alongside light at its speed. From the fact that Maxwell's equations of electromagnetism do not allow for a stationary electromagnetic wave, he deduced that there was something wrong with Newtonian conceptions and not with Maxwell's theory. None of the other greats of this era, Lorentz or Poincare saw the matter with as much penetrating clarity as this totally unknown worker at the Patent office in Berne. Einstein looked to the experiments for verification of his intuition and not as their origin.
The conclusion is astonishing in its implications. This means that Einstein was guided more by his own thoughts and intuition than by experiment. The crisis physics found itself in, led not to more complications, but to a simplification of its foundations. This, I've realized gives the true measure of the man's achievement. Surely, this is what Erwin Schrodinger had in mind when he said," The task is, not so much to see what no one has yet seen; but to think what nobody has yet thought, about that which everybody sees."
To my utter amazement, I found that the phenomenon of dependence of time intervals on relative velocity, could be derived by using nothing more than a theorem which every school kid is familiar with - the Pythagorus' theorem.
Poincaré wrote in the sense of his conventionalist philosophy in 1889: "Whether the ether exists or not matters little - let us leave that to the metaphysicians; what is essential for us is, that everything happens as if it existed, and that this hypothesis is found to be suitable for the explanation of phenomena. After all, have we any other reason for believing in the existence of material objects? That, too, is only a convenient hypothesis; only, it will never cease to be so, while some day, no doubt, the ether will be thrown aside as useless."
He also denied the existence of absolute space and time by saying in 1901: "1. There is no absolute space, and we only conceive of relative motion ; and yet in most cases mechanical facts are enunciated as if there is an absolute space to which they can be referred. 2. There is no absolute time. When we say that two periods are equal, the statement has no meaning, and can only acquire a meaning by a convention. 3. Not only have we no direct intuition of the equality of two periods, but we have not even direct intuition of the simultaneity of two events occurring in two different places. I have explained this in an article entitled "Mesure du Temps" [1898]. 4. Finally, is not our Euclidean geometry in itself only a kind of convention of language?"
However, Poincaré himself never abandoned the ether hypothesis and stated in 1900: "Does our ether actually exist ? We know the origin of our belief in the ether. If light takes several years to reach us from a distant star, it is no longer on the star, nor is it on the earth. It must be somewhere, and supported, so to speak, by some material agency." And referring to the Fizeau experiment, he even wrote: "The ether is all but in our grasp." He also said the ether is necessary to harmonize Lorentz's theory with Newton's third law. Even in 1912 in a paper called "The Quantum theory", Poincaré ten times used the word "ether", and described light as "luminous vibrations of the ether".Poincaré, Henri (1908/13), "The New Mechanics" ref by Giannetto in Poincaré's Electromagnetic Quantum Mechanics. And in 1906 Planck worked out the 'new mechanics' predicted by Poincaré, in What is wrong with relativity.Today some physicists want to adopt a new convention. It is not that they are constrained to do so; they consider this new convention more convenient; that is all.
Poincaré's radiation paradox can simply be solved by applying Einstein's equivalence. If the light source loses mass during the emission by E / c2, the contradiction in the momentum law vanishes without the need of any compensating effect in the ether.
Similar to Poincaré, Einstein concluded in 1906 that the inertia of (electromagnetic) energy is a necessary condition for the center of mass theorem to hold in systems, in which electromagnetic fields and matter are acting on each other. Based on the mass–energy equivalence he showed that emission and absorption of em-radiation and therefore the transport of inertia solves all problems. On that occasion, Einstein referred to Poincaré's 1900-paper and wrote:
| Although the simple formal views, which must be accomplished for the proof of this statement, are already mainly contained in a work by H. Poincaré [Lorentz-Festschrift, p. 252, 1900], for the sake of clarity I won't rely on that work. |
But Poincare had great insights.
Arthur I. Miller 1981: Poincaré distinguished (in July 1905 paper) between "ideal" and "real" systems and electrons. That is, Lorentz's and Poincaré's usage of reference frames lacks an unambiguous physical interpretation, because in many cases they are only mathematical tools, while in Einstein's theory the processes in inertial frames are not only mathematically, but also physically equivalent.
- p. 172: "Although Poincaré's principle of relativity is stated in a manner similar to Einstein's, the difference in content is sharp. The critical difference is that Poincaré's principle admits the existence of the ether, and so considers the velocity of light to be exactly c only when it is measured in coordinate systems at rest in the ether. In inertial reference systems, the velocity of light is c and is independent of the emitter's motion as a result of certain compensatory effects such as the mathematical local time and the hypothesis of an unobservable contraction. Consequently, Poincaré's extension of the relativity principle of relative motion into the dynamics of the electron resided in electromagnetic theory, and not in mechanics...Poincaré came closest to rendering electrodynamics consistent, but not to a relativity theory." p. 217: "Poincaré related the imaginary system Σ' to the ether fixed system S' ".
Nowadays, we do not speak about ether. But is the situation better with the vacuum of quantum field theory, the cosmological constant, dark energy, and so on... ? Light is the only wave (photon) that is self-sustaining by the electromagnetic duality, and needs no support from the environment, is said? Really? With deBroglie packages, quanta? The unknowable, Gödel, etc. See Luis Gonzalez-Mestres Cosmic rays and tests of fundamental principles.
In "Relativity and Its Roots" By Banesh Hoffmann
Moreover, if light consists of particles, as Einstein had suggested in his paper submitted just thirteen weeks before this one, the second principle seems absurd: A stone thrown from a speeding train can do far more damage than one thrown from a train at rest; the speed of the particle is not independent of the motion of the object emitting it. And if we take light to consist of particles and assume that these particles obey Newton's laws, they will conform to Newtonian relativity and thus automatically account for the null result of the Michelson-Morley experiment without recourse to contracting lengths, local time, or Lorentz transformations. Yet, as we have seen, Einstein resisted the temptation to account for the null result in terms of particles of light and simple, familiar Newtonian ideas, and introduced as his second postulate something that was more or less obvious when thought of in terms of waves in an ether.
Walter, S. (2007). Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910.
The law of gravitational attraction is a window on three formal approaches to laws of nature based on Lorentz-invariance : Poincaré’s four-dimensional vector space (1906), Minkowski’s matrix calculus and spacetime geometry (1908), and Sommerfeld’s 4-vector algebra (1910). In virtue of a common appeal to 4-vectors for the characterization of gravitational attraction, these three contributions track the emergence and early development of four-dimensional physics.
In July, 1905, Henri Poincaré proposed two laws of gravitational attraction compatible with the principle of relativity and all astronomical observations explained by Newton’s law. Two years later, in the fall of 1907, Albert Einstein began to investigate the consequences of the principle of equivalence for the behavior of light rays in a gravitational field. The following year, Hermann Minkowski , Einstein’s former mathematics instructor, borrowed Poincaré’s notion of a four-dimensional vector space for his new matrix calculus, in which he expressed a novel theory of the electrodynamics of moving media, a spacetime mechanics, and two laws of gravitational attraction. Following another two-year hiatus, Arnold Sommerfeld characterized the relationship between the laws proposed by Poincaré and Minkowski, calling for this purpose both on spacetime diagrams and a new 4-vector formalism. Of these four efforts to capture gravitation in a relativistic framework, Einstein’s has attracted the lion’s share of attention, and understandably so in hindsight, but at the expense of a full understanding of what is arguably the most significant innovation in contemporary mathematical physics : the four-dimensional approach to laws of physics
As we saw Einstein did not got the Nobel for GR, but for the photoelectric effect (the light particle duality), and his theory was mainly seen as a theory of signals. The relativity has no Nobelist. Niels Bohr got the prize after him, Max Planck 1918 and Robert Millikan next year 1923. As Einstein later recalled: The new feature was the realization that the bearing of the Lorentz transformation transcended its connection with Maxwell's equations and was concerned with the nature of space and time in general.
Arthur Eddington, who led the expedition to prove Einstein’s Theory of Relativity, they had a lot in common: “[the speed of light] is the speed at which the mass of matter becomes infinite,” where “lengths contract to zero” and—most surprisingly—where “clocks stand still.”
British scientist Arthur Eddington was one of the most prominent astrophysicists and was Director of the Cambridge Observatory, a seat originally held by the father of British science, Sir Isaac Newton. The then obscure German theorist Albert Einstein had spent years working on his General Theory of Relativity, a theory that threatened two centuries of Newtonian certainty and the foundations of British science.
Albert Einstein 1905: On The Electrodynamics of Moving Bodies.A note: Eddington believed he had identified an algebraic basis for fundamental physics, which he termed "E-frames" (representing a certain group – a Clifford algebra). While his theory has long been neglected by the general physics community, similar algebraic notions underlie many modern attempts at a grand unified theory. Moreover, Eddington's emphasis on the values of the fundamental constants, and specifically upon dimensionless numbers derived from them, is nowadays a central concern of physics.
Arthur Eddington, 1929: The Nature of the Physical World.
- 1936. Relativity Theory of Protons and Electrons.
Banesh Hoffmann, Relativity and Its Roots"
Jacques. Fric (June 2003). Henri Poincaré : A decisive contribution to Special Relativity: The short story
Enrico Giannetto, 1998. The rise of Special Relativity: Henri Poincaré’s works before Einstein.
Robert Resnick, An Introduction to Special Relativity
His basic approach was to combine several fundamental constants in order to produce a dimensionless number. In many cases these would result in numbers close to 10, its square, or its square root. He was convinced that the mass of the proton and the charge of the electron were a natural and complete specification for constructing a Universe and that their values were not accidental. One of the discoverers of quantum mechanics, Paul Dirac, also pursued this line of investigation, which has become known as the Dirac large numbers hypothesis, and some scientists even today believe it has something to it.
A somewhat damaging statement in his defence of these concepts involved the fine structure constant, α. At the time it was measured to be very close to 1/136, and he argued that the value should in fact be exactly 1/136 for epistemological reasons. Later measurements placed the value much closer to 1/137, at which point he switched his line of reasoning to argue that one more should be added to the degrees of freedom, so that the value should in fact be exactly 1/137, the Eddington number. Wags at the time started calling him "Arthur Adding-one"Penrose writes: In the 1930s, even general relativity was not regarded as a worthy activity for aspiring astrophysicists to devote themselves to.
Was Einstein plagiarizing the ideas?
" Henri Poincare predicted that gravity propagates at light speed, in 1905, and created the first relativistic (scalar) covariant theory of gravitation, long before Einstein plagiarized his ideas."? Plagiatry some think?
Tesla (81 y old) had completed a "dynamic theory of gravity". He stated that it was "worked out in all details" and that he hoped to soon give it to the world. The theory was never published.
The bulk of the theory was developed between 1892 and 1894, during the period that he was conducting experiments with high frequency and high potential electromagnetism and patenting devices for their use. Reminiscent of Mach's principle, Tesla stated in 1925 that:
There is nothing endowed with life—from man, who is enslaving the elements, to the nimblest creature—in all this world that does not sway in its turn. Whenever action is born from force, though it be infinitesimal, the cosmic balance is upset and the universal motion results.
Tesla was critical of Einstein's relativity work, calling it:
...[a] magnificent mathematical garb which fascinates, dazzles and makes people blind to the underlying errors. The theory is like a beggar clothed in purple whom ignorant people take for a king ... its exponents are brilliant men but they are metaphysicists rather than scientists ...
Tesla also argued:
I hold that space cannot be curved, for the simple reason that it can have no properties. It might as well be said that God has properties. He has not, but only attributes and these are of our own making. Of properties we can only speak when dealing with matter filling the space. To say that in the presence of large bodies space becomes curved is equivalent to stating that something can act upon nothing. I, for one, refuse to subscribe to such a view.
Tesla also believed that much of Albert Einstein's relativity theory had already been proposed by Ruđer Bošković, stating in an unpublished interview:
Einstein struggled with these ideas, on and off,f or ten long years, before he finally found the answer. Further, he did all of this on his own, with essentially no contact with any other physicist.That is often said. But is it true? Look:...the relativity theory, by the way, is much older than its present proponents. It was advanced over 200 years ago by my illustrious countryman Ruđer Bošković, the great philosopher, who, notwithstanding other and multifold obligations, wrote a thousand volumes of excellent literature on a vast variety of subjects. Bošković dealt with relativity, including the so-called time-space continuum ...'
At the end of June 1915 Einstein spent a week at the University Göttingen where he lectured for six two-hour sessions on his (still incorrect) October 1914 version of what would become general relativity. Two of those present were colossi in the world of mathematics, David Hilbert and Felix Klein. "To my great joy," Einstein later recalled, "I succeeded in convincing Hilbert and Klein completely." Shortly after, Einstein and Hilbert began an intense exchange of letters on the outstanding problems in Einstein's theory. And now matters quickly came to a head. After chopping and changing the equations in his theory several times in the autumn of 1915 – totally confusing his scientific colleagues in the process – Einstein made a monumental breakthrough.
On November 18, 1915, he applied his new theory of gravitation to the old problem of Mercury's orbit and, lo and behold, found that it predicted, for the extra advance of the perihelion, exactly the 43 arc-seconds per century that astronomers had measured and that had foiled every other attempt at explanation. "For a few days," he remembered, "I was beside myself with joyous excitement." To Hilbert, he wrote: "Today I am presenting to the [Prussian] Academy a paper in which I derive quantitatively out of general relativity, without any guiding hypothesis, the perihelion motion of Mercury discovered by Leverrier. No gravitation theory had achieved this until now." The Mercury figure was correct, but not yet the precise formulation. On November 25, Einstein submitted yet another paper, called "The Field Equations of Gravitation," which at last contained the correct mathematical scaffolding of general relativity. There's a postscript. Five days earlier, Hilbert had submitted a paper to a journal in Göttingen containing exactly the same field equations. Suggestions have been made that Hilbert plagiarized Einstein, or perhaps vice versa; certainly over those final frantic weeks before publication, each man came to know the other's thoughts well. But if the relationship between Einstein and Hilbert was strained for a while over the question of priority, it ended amicably enough and Hilbert was able to write: "Every boy in the streets of Göttingen understands more about four-dimensional geometry than Einstein. Yet, in spite of that, Einstein did the work and not the mathematician."Spinor and spinor fields.
Used in the theory of the orthogonal groups (such as the rotation or the Lorentz groups), spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors. However, spinors transform well under the infinitesimal orthogonal transformations (like infinitesimal rotations or infinitesimal Lorentz transformations). Under the full orthogonal group, however, they do not quite transform well, but only "up to a sign". This means that a 360 degree rotation transforms a spinor into its negative, and so it takes a rotation of 720 degrees for a spinor to be transformed into itself. Spinors are objects associated to a vector space with a quadratic form (like Euclidean space with the standard metric or Minkowski space with the Lorentz metric), and are realized as elements of representation spaces of Clifford algebras. For a given quadratic form, several different spaces of spinors with extra properties may exist. Later, spinors were adopted by quantum mechanics in order to study the properties of the intrinsic angular momentum. The most typical type of spinor, the Dirac spinor, is an element of the fundamental representation of the complexified Clifford algebra Cℓ(p, q), into which the spin group Spin(p, q) may be embedded. On a 2k- or 2k+1-dimensional space a Dirac spinor may be represented as a vector of 2k complex numbers. The Lie algebra so(V, g) is embedded as a Lie subalgebra in Cℓ(V, g) equipped with the Clifford algebra commutator as Lie bracket. Therefore, the space Δ is also a Lie algebra representation of so(V, g) called a spin representation. If n is odd, this representation is irreducible. If n is even, it splits again into two irreducible representations Δ = Δ+ ⊕ Δ− called the half-spin representations.
With the Clifford action but with contraction using the hermitian form, this construction gives a spinor space at every point of an almost Hermitian manifold and is the reason why every almost complex manifold (in particular every symplectic manifold) has a Spinc structure. Likewise, every complex vector bundle on a manifold carries a Spinc structure.[Lawson & Michelsohn 1989,]
In particle physics, a spinor field of order 2s describes a particle of spin s, where s is an integer or half-integer. Therefore, a spinor of order 2s contains as much information as a tensor of order s. As a result of this, particles of integer spin (bosons) can be described equally well by tensor fields or spinor fields, whereas particles of half-integer spin (fermions) can be described only by spinor fields.
Spinor fields describing particles of zero rest mass satisfy the so-called zero rest mass equation. Examples of zero rest mass particles include the gauge bosons (as long as gauge symmetry is not violated) such as the photon and possibly one of the neutrinos (a fermion). Primed spinors transform under the conjugate of the transformation for unprimed ones, Einstein summation is used throughout, and nabla denotes the spinor, which is equivalent to the Levi-Civita connection on Minkowski space.Spinors in three dimensions,The perturbative approach to the Einstein equations leads to equations which are essentially identical with Maxwell's equations. (These are not so important in Poincare's model a la TGD, instead light-like 4-surfaces there).
Quaternions and spatial rotation
Fock space - creating spinors using anti-commuting creation operators in W acting on a vacuum ω.
Bott periodicity.
Cartan, Élie (1966), The theory of spinors, Paris, Hermann (reprinted 1981, Dover Publications).
Penrose, Roger; Rindler, W. (1988), Spinors and Space-Time: Volume 2, Spinor and Twistor Methods in Space-Time Geometry, Cambridge University Press.
Said, Salem. "Zero Rest Mass Equation". MathWorld.
R. Sverdlov; A Geometrical Description of Spinor Fields; arXiv:0802.1914
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. Of the four equations, two of them, Gauss's law and Gauss's law for magnetism, describe how the fields emanate from charges. For the magnetic field there is no magnetic charge and therefore magnetic fields lines neither begin nor end anywhere. The other two equations describe how the fields 'circulate' around their respective sources; the magnetic field 'circulates' around electric currents and time varying electric field in Ampère's law with Maxwell's correction, while the electric field 'circulates' around time varying magnetic fields in Faraday's law.
Henri Poincaré developed Lorentz's theory of electrons to a state formally equivalent to the theory published at the same time by Einstein. Poincaré and Einstein both recognized that the Lorentz transformations (named by Poincaré) form a group; Poincaré alone exploited this knowledge in the search for invariants. Among Poincaré's insights relating to his introduction of a fourth imaginary coordinate in t sqrt-1 (where c=1), was the recognition of a Lorentz transformation as a rotation about the origin in four-dimensional space, and the invariance of the sum of squares in this space, which he described as a measure of distance (1906: 542).
This analysis then formed the basis of his evaluation of the possibility of a Lorentz-covariant theory of gravitation.
Poincare said 1909 that the equivalence of all inertial frames combined with the invariance of (two-way) light speed were sufficient to infer Einstein's model. He maintained that one must also stipulate a particular contraction of physical objects in their direction of motion. This is sometimes cited as evidence that Poincare still failed to understand the situation, but there's a sense in which he was actually correct. The two famous principles of Einstein's 1905 paper are not sufficient to uniquely identify special relativity, as Einstein himself later acknowledged
Minkowski space as a modern affine space views space as a homogeneous space of the Poincaré group with the Lorentz group as the stabilizer.
The Poincaré group is the group of isometries of Minkowski spacetime (SR). It is a 10-dimensional noncompact Lie group. The abelian group of translations is a normal subgroup while the Lorentz group is a subgroup, the stabilizer of a point.
Another way of putting it is that the Poincaré group is a group extension of the Lorentz group by a vector representation of it.
Vectors, scalars, tensors... as operators. Stability and harmony.It was shown by Poincaré that the argument of Pierre-Simon Laplace, ('Newton of France'), who argued that the speed of gravity is many times faster (but not instantaneous) than the speed of light, is not valid within a relativistic theory.
That is, said Abraham, in a relativistic theory of gravitation, planetary orbits are stable (no divine help needed for the stability) even when the speed of gravity is equal to that of light.
In 1776, Laplace published a memoir in which he first explored the possible influences of a purported luminiferous ether or of a law of gravitation that did not act instantaneously. He ultimately returned to an intellectual investment in Newtonian gravity. Euler and Lagrange had made a practical approximation by ignoring small terms in the equations of motion. Laplace noted that though the terms themselves were small, when integrated over time they could become important. Laplace carried his analysis into the higher-order terms, up to and including the cubic. Using this more exact analysis, Laplace concluded that any two planets and the sun must be in mutual equilibrium and thereby launched his work on the stability of the solar system. In 1783, Part II of Théorie du Mouvement et de la figure elliptique des planètes in 1784, and in the third volume of the Mécanique céleste, Laplace completely determined the attraction of a spheroid on a particle outside it. This is memorable for the introduction into analysis of spherical harmonics or Laplace's coefficients, and also for the development of the use of what we would now call the gravitational potential in celestial mechanics.About Poincare gravity and non-Euclidean space. In 1905 and 1906 Poincaré pointed out the possibility of a gravitational theory, in which changes propagate with the speed of light and which is Lorentz covariant. He pointed out that in such a theory the gravitational force not only depends on the masses and their mutual distance, but also on their velocities and their position due to the finite propagation time of interaction. On that occasion Poincaré introduced four-vectors. Similar models as that of Poincaré were discussed by Minkowski (1907) and Sommerfeld (1910). They tried to modify Newton's theory and to establish a Lorentz invariant gravitational law, in which the speed of gravity is that of light, but like in Lorentz's model the value for the perihelion advance of Mercury was much too low, (the actual advance is only 43 seconds of arc per century.). It was shown by Abraham (1912) that those models belong to the class of "vector theories" of gravitation (Newton used geometric reasoning). The fundamental defect of those theories is that they implicitly contain a negative value for the gravitational energy in the vicinity of matter, which would violate the energy principle.
Antimatter is not the answer of that negative value because it also gravitate, and have the same mass. There are efforts to determine this issue today, with a search for antigravity, non-gravitional theories and gravitional waves. Negative energy is also discussed, among all in stability of black holes. We shall look at this problem later. This is a serious problem for Poincare gravity. Can it be linked to time dilation?
As an alternative, Abraham (1912) and Gustav Mie (1913) proposed different "scalar theories" of gravitation. While Mie never formulated his theory in a consistent way, Abraham completely gave up the concept of Lorentz-covariance (even locally), and therefore it was irreconcilable with relativity. In addition, all of those models violated the equivalence principle, and Einstein argued that it is impossible to formulate a theory which is both Lorentz-covariant and satisfies the equivalence principle.
However, finnish Gunnar Nordström (1913) was able to create a model which fulfilled both conditions, by making both the gravitational and the inertial mass dependent on the gravitational potential. Nordström's theory of gravitation was remarkable because it was shown by Einstein and Adriaan Fokker (1914, 1920), that in this model gravitation, a metric theory of gravitation, can be completely described in terms of spacetime curvature. The effects of gravitation are treated entirely in terms of the geometry of a curved spacetime. Although Nordström's theory is without contradiction, from Einstein's point of view a fundamental problem persisted: It doesn't fulfill the important condition of general covariance, as in this theory preferred frames of referenced can still be formulated.
So contrary to those "scalar theories", Einstein (1911–1915) developed a "tensor theory" (i.e. GR), which fulfills both the equivalence principle and general covariance. As a consequence, the notion of a complete "special relativistic" theory of gravitation had to be given up, as in GR the constancy of light speed (and Lorentz covariance) is only locally valid.
The shape of the Universe, the flatness problem.
This is the big problem. GR is incompatible with SR. Gravity was left out from SR. Did they give up too easily? This is linked to the spin and to the flatness problem of fine-tuning, as some of the initial conditions of the universe appear to be fine-tuned to very 'special' values. The parameter which appears fine-tuned is among all the density of matter and energy in the universe (Ω). This value affects the curvature of space-time. The problem was first mentioned by Robert Dicke in 1969.
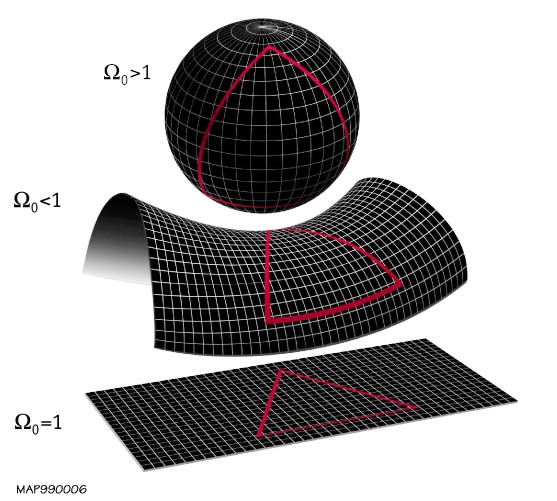The local geometry of the universe is determined by whether the relative density Ω is less than, equal to or greater than 1. From top to bottom: a spherical universe with greater than critical density (Ω>1, k>0); a hyperbolic, underdense universe (Ω<1, k<0); and a flat universe with exactly the critical density (Ω=1, k=0).A positively curved universe is described by spherical geometry, and can be thought of as a three-dimensional hypersphere, or some other spherical 3-manifold (such as the Poincaré dodecahedral space), all of which are quotients of the 3-sphere. See also the three body problem. (the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then determining the motions of the three bodies, in accordance with the laws of classical mechanics: Newton's laws of motion and of universal gravitation.)
According to Nordström, in a vacuum region only the semi-traceless part of the Riemann tensor can be nonvanishing. Then our covariant differential constraint on Sab shows how variations in the trace of the stress-energy tensor in our spacetime model can generate a nonzero trace-free Ricci tensor, and thus nonzero semi-traceless curvature, which can propagate into a vacuum region. This is critically important, because otherwise gravitation would not, according to this theory, be a long-range force capable of propagating through a vacuum.
Note - this would create a push instead of a pull. Something like the adiabatic force?
In GR, something alike happens, but there it is the Ricci tensor which vanishes in any vacuum region, but not in a region which is matter-free but contains an electromagnetic field, and it is the Weyl curvature which is generated (via another first order covariant differential equation) by variations in the stress-energy tensor and which then propagates into vacuum regions, rendering gravitation a long-range force capable of propagating through a vacuum.
Another very striking feature of Nordström's theory is that it while it can be written as the theory of a certain scalar field in Minkowski spacetime, with the expected conservation law for nongravitational mass-energy together with gravitational field energy, but suffers from a not very memorable force law, in the curved spacetime formulation the motion of test particles is very elegantly described (the world line of a free test particle is a timelike geodesic, and by an obvious limit, the world line of a laser pulse is a null geodesic, see next post for explanation of worldline/timeline), but we lose the conservation law. So which interpretation is correct? In other words, which metric is the one which according to Nordström can be measured locally by physical experiments? The answer is: the curved spacetime is the physically observable one in this theory (as in all metric theories of gravitation); the flat background is a mere mathematical fiction which is however of inestimable value for such purposes as writing down the general vacuum solution, or studying the weak field limit. History of SR, Nordström theory of gravitation.Nordström, Gunnar (1913), "Zur Theorie der Gravitation vom Standpunkt des Relativitätsprinzips", Annalen der Physik 347 (13): 533–554Compression, extension, deformation...
Jean Eisenstaedt, Anne J. Kox (1988). Studies in the History of General Relativity
Fokker was convinced that space and time should not be treated in the same way, so he suggested the term chronogeometry, separation of space and time, for GR. In SR he defined the dynamical center of mass, Fokker action. Here at university course. GR is a more general theory than SR.
Contraction - dilation could also be explained as compression - extension? The extensions of the Poincar´e algebra (also to supersymmetry) are obtained from a “square root” of the translations, and built on Lie-algebra or -derivates. The generators of the Poincar´e algebra are obtained as three-fold symmetric products of more fundamental generators, leading to the “cubic root” of translation. Surface integrals, amplitudes, etc. This is an important notation, giving deformation (below and here, and here).
If all of physics is really Lorentz-invariant, we shall never be able to measure the "absolute" velocity V, so that the difference between the "true" simultaneity (that defined in the preferred inertial frame E) and the "artificial" ones (those defined in the other inertial frames F) will remain at the metaphysical level. In that case, one may indeed qualify the concept of ether as "superfluous", as Einstein (1905) put it. This means that past, present and future are relative notions, and that time travels are at least theoretically possible. It also enforces to consider this mixture of space and time as the true arena for physical theories. In particular, it may lead (though not in a compelling way) to GR, according to which gravitation is the curvature of space-time, and in which free test particles follow the geodesics of a pseudo-Riemannian metric on space-time. [If GR is correct, then, according to Bonnor (2002), time travels are indeed quite plausible.] In my opinion, this is no physical explanation of gravity. Moreover, GR's invariance under arbitrary coordinate changes is antinomic to quantum theory, in which, in particular, the choice of the time coordinate cannot be arbitrary. This leads to the longstanding difficulties with quantum gravity, which the mainstream researchers want to overcome by going into string- and M-theories with their many-dimensional manifolds. One should be allowed to explore simpler possibilities.See the phase space, solving time-dependent differential equations.
There is indeed another possibility, which seems to have been little explored before: that not all of physics is subjected to the relativity principle, and that the force which contradicts relativity is precisely gravitation. This possibility exists only in the Lorentz-Poincaré version of SR, that sees SR as a consequence of the Lorentz contraction: it obviously doesn't exist if the reason for SR is the universal validity of the relativity principle, as in Einstein's version. Why should gravitation be the range of a such violation? Simply because SR really doesn't include gravitation. After all, even in GR, the relativity principle of SR does not hold true.
Thus, by expressing quantum mechanics in phase space (the same ambit as for classical mechanics), the Weyl map facilitates recognition of quantum mechanics as a deformation (generalization) of classical mechanics, with deformation parameter ħ/S, where S is the action of the relevant process. (Other familiar deformations in physics involve the deformation of classical Newtonian into relativistic mechanics, with deformation parameter v/c; or the deformation of Newtonian gravity into GR, with deformation parameter Schwarzschild-radius/characteristic-dimension.)
Time is also compressed or extended (by gravity, em-radiation) and as a consequence also the metric? It is fair to say that what Einstein did is that he replaced the absoluteness of time and of space with the absoluteness of the speed of light. The Speed of Light is more fundamental than time and space. Light is not homogenous, but holographic with time-frequency, consisting of three parts , maybe four. Time, space and light imbeddings of an observer, creating tensions through motion? Gravity??? Giving the four forces?
Theorema Egregium − The "remarkable theorem" discovered by Gauss which showed there is an intrinsic notion of curvature for surfaces. This is used by Riemann to generalize the (intrinsic) notion of curvature to higher dimensional spaces.
Einstein 1905: Annalen der Physik vol XVII 1905 p 891-921: ref 6. and vol XVIII, p 639-641 http://www.nobelprize.org/nobel_prizes/physics/laureates/1921/
Lorentz, H.A. (1900). "Considerations on Gravitation"
Maxwell, James Clerk, "A Dynamical Theory of the Electromagnetic Field". Philosophical Transactions of the Royal Society of London 155, 459-512 (1865).
Hendrik Lorentz (1904) "Electromagnetic phenomena in a system moving with any velocity less than that of light", Proc. Acad. Science Amsterdam, IV, 669-78. Maxwell's equations, a wiki book.
A.D.Fokker, Albert Einstein, inventor of chronogeometry. Synthese Vol. 9, No. 6A/6B, 1953/1955
Naber, G. L., 1992. The Geometry of Minowski Spacetime. Springer.
I have only linked to main sources. In the text are numerous links, mostly to wikipedia, not referenced in any other way. Please follow the hyperlinks.
